私が指導する際に伝えていることを参考にしてみてください!
濃度から重さを求める
中学受験を乗り越えるうえで避けられないのが算数です。
算数を苦手とする小学生は多いです。
そんな親御さんも含め小学生でも理解できるように、問題の解き方を基本から解説しています。
前回は、「濃度とは何か?」について書きました。

今回は、前回学んだ濃度という考え方をもとに、重さを出す問題を解いてみましょう。
濃度から食塩・水・食塩水の重さを求める
<基礎問題2>
5%の食塩水400 gには何gの食塩が溶けていますか。
<基礎問題3>
4%の食塩水300 g作るには何gの水が必要ですか。
<基礎問題4>
12%の食塩水から30gの食塩をとるには何gの食塩水が必要ですか。
今回は、この3つの問題を考えてみましょう。
では、まず<基礎問題2>からです。
前回の復習
前回濃度の考え方を説明しました。
濃度とは、溶けているものの濃さを数値化したものです。
百分率を利用して濃度を表すと、全体を100としたときの溶けているものの数のことです。
たとえば、次の図を見てください。
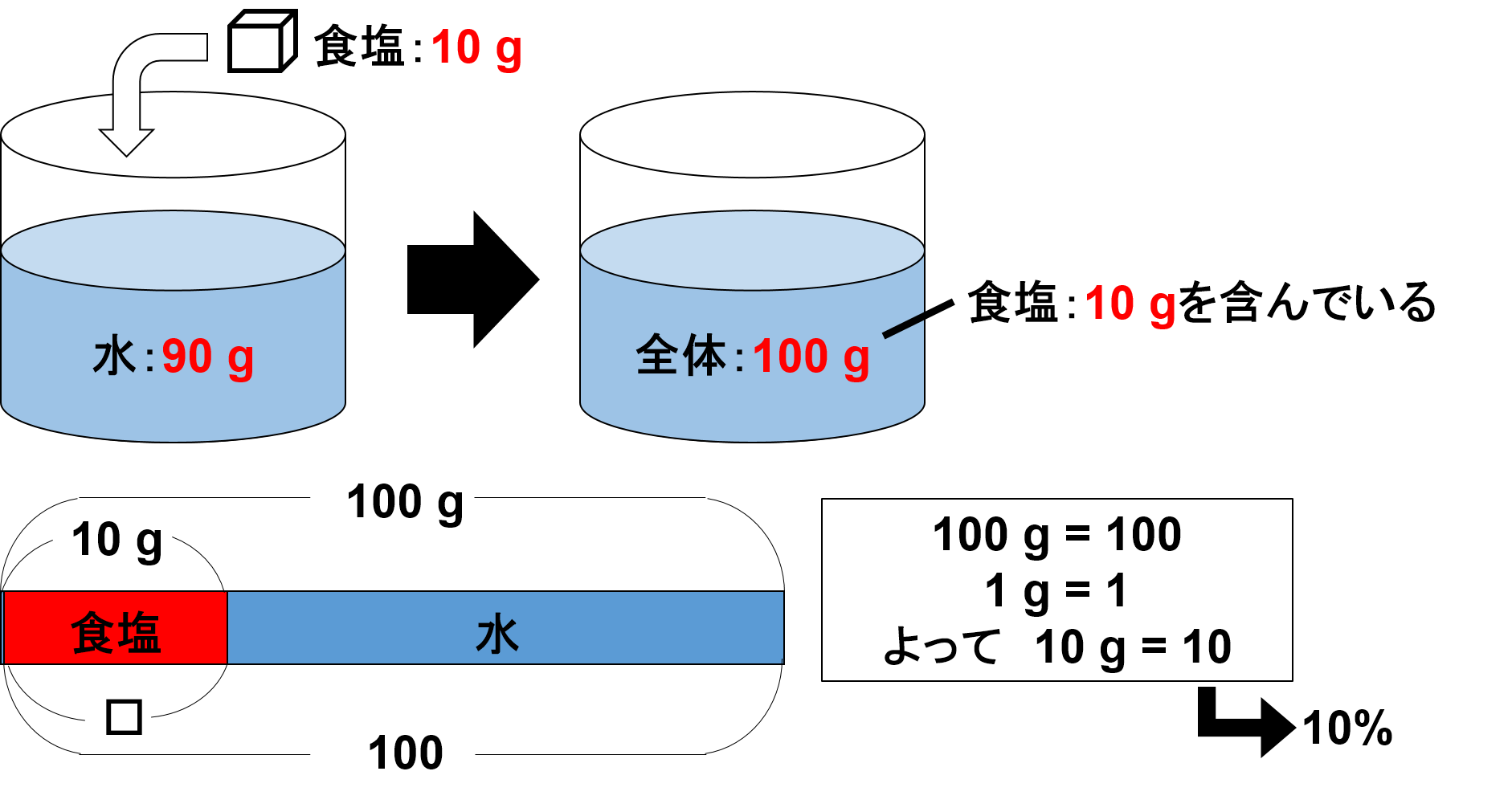
この場合、濃度は10%ということになります。
全体を100としたときにどれくらい入っているかを示したのがは百分率
濃さを数値化したものが濃度
では、濃度から食塩の重さを求めるにはどうすればいいかを見ていきましょう。
濃度から食塩の重さを求める
5%の食塩水400 gには何gの食塩が溶けていますか。
5%ということは、全体を100としたときに食塩の重さは5ですということです。
これを図で表してみましょう。

全体を100としているので、100にあたるのが400 gです。
そして1にあたるのが4 gですので、今回の濃度5にあたるのは20 gということになります。
よって、以下の図の様に380 gの水に食塩を20 g加えて5%の濃度の食塩水が作られていたということになります。

濃度から水の重さを求める
続いて、濃度から食塩水を作るのに必要な水の重さを求めています。
4%の食塩水300 g作るには何gの水が必要ですか。
先ほどと同じように図で表してみます。

4%の食塩水ですので、全体を100としたとき食塩の重さにあたるのは4です。
今回求めるのは水の重さですので、全体を100とすると水の重さにあたるのは100 – 4 = 96になります。
後は先ほどと同じように、100が300 gですので、1が3 gになります。
よって、水にあたる96は288 gということになります。
もちろん、食塩の重さを求めて全体から引けば水の重さは出せます。
ですが、今後水の量を使って問題を解くことがありますので今回は水の量を直接出す方法を用いました。

濃度から食塩水の重さを求める
では続いて、濃度から食塩水の重さを求めてみましょう。
12%の食塩水から30gの食塩をとるには何gの食塩水が必要ですか。
先ほどと同じように下の図で考えてみましょう。
今回は全体の重さがわかっていないので、食塩の重さから考えることになります。

濃度12にあたるのが食塩の重さ30 gです。
そして、1にあたるのが2.5 gですので、全体の100に当たるのは250 gになります。
つまり、12%の食塩水は250gの中に30 gの食塩が入っているということになります。

今回は、濃度を用いて食塩・水・食塩水の重さを求める方法について書きました。
今後、「水を蒸発させる」「食塩を加える」「異なる濃度の食塩水を混ぜる」問題などを解いていきます。
その際に、ここまで扱ってきた<基本問題1>~<基本問題4>を用います。
まずは、この<基本問題1>~<基本問題4>をしっかり理解できるようにしてください。
次回は、「水を蒸発させる」「水を加える」問題を扱います。
食塩水問題の基礎的な考え方はこちら↓





