『相当算』
中学受験を乗り越えるうえで避けられないのが算数です。
算数を苦手とする小学生は多いです。
そんな親御さんも含め小学生でも理解できるように、問題の解き方を基本から解説しています。
今まで複数回に分けて、「旅人算」「食塩水の問題」「仕事算」「過不足算」の基本的な考え方について書いてきました。
旅人算:同じ向きと逆向きに歩く違い
食塩水:濃度とは?百分率とは?
仕事算:1日の仕事量は?
過不足算:過不足算の基本について
今回は、「相当算」の基本的な考え方について書いていきたいと思います。
相当算の基本問題:比から求める問題
相当算を解くうえでよく出てくるのが、「比」を用いる問題です。
比を考えることで解けるようになる問題がとても多いです。
今回は、比から求める問題について考えてみましょう。
<基本問題1>
ある学校では、男子の人数は女子の人数より42人多く、さらに、男子の$ \frac{7}{18} $と女子の$ \frac{5}{12} $の人数が等しくなります。
では、<基本問題1>の基礎的な考え方か見ていきましょう。
男女の人数の比を考える。
まず、例題を使って比について考えてみましょう。
ある学校では、男子の$ \frac{7}{18} $と女子の$ \frac{5}{12} $の人数が等しくなります。この学校の男女比はどうなりますか。
次の図を見てください。
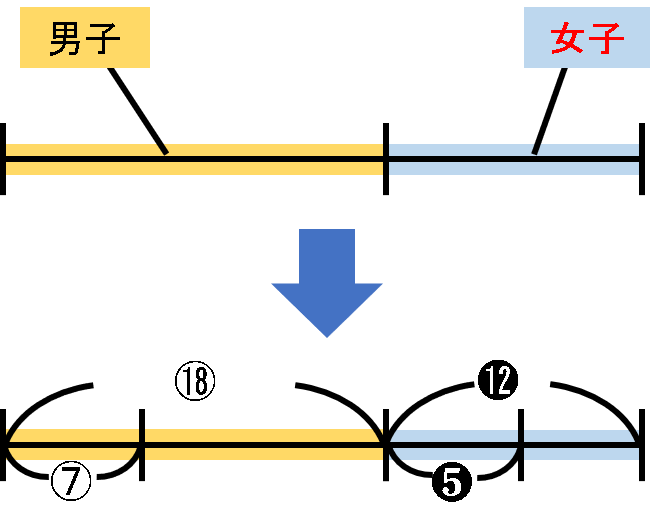
男子の$ \frac{7}{18} $とは全体をとしたうちの⑱としたうちの⑦であり、女子の$ \frac{5}{12} $とは全体を、➁としたうちの❺となります。
ここで、男子全体と女子全体では人数が異なりますので違う文字を用いています。
今回の問題では、⑦と❺が同じという事になっています。
しかし、それぞれの数字が異なってしまっています。
ここで用いるのが最小公倍数の考え方です。
今回は7と5の最小公倍数なので、35を用います。
そのため、⑦は5倍、❺は7倍します。
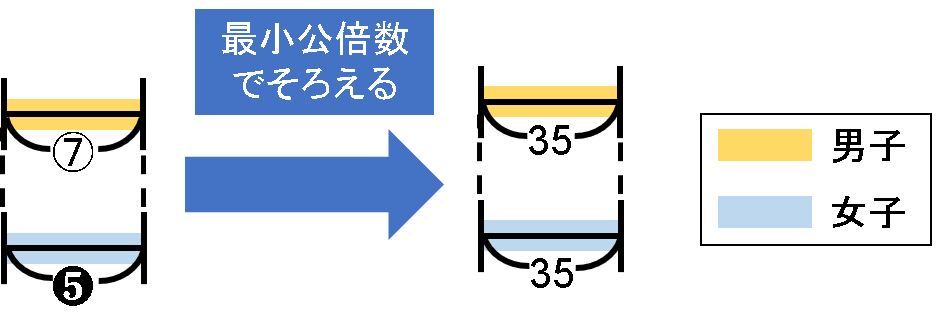
それに伴い、全体の⑱と➀もそれぞれ5倍、7倍します。
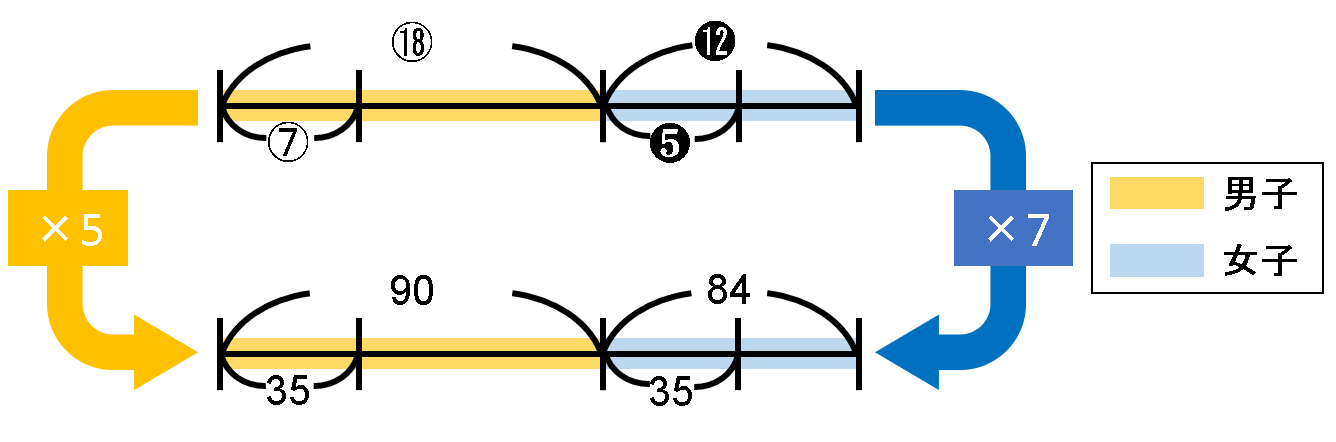
同じ人数を同じ文字であらわすことにより、男子全体と女子全体も比較することができるようになります。
よって、<例題1>の答えは、$ 90 : 84 = 15 : 14 $ということになります。
男女の比から全体を出す
<例題>により男女の人数比が出せました。
この比を用いることで、男女の人数の差から全体を求めることができます。
次の図を見てください。
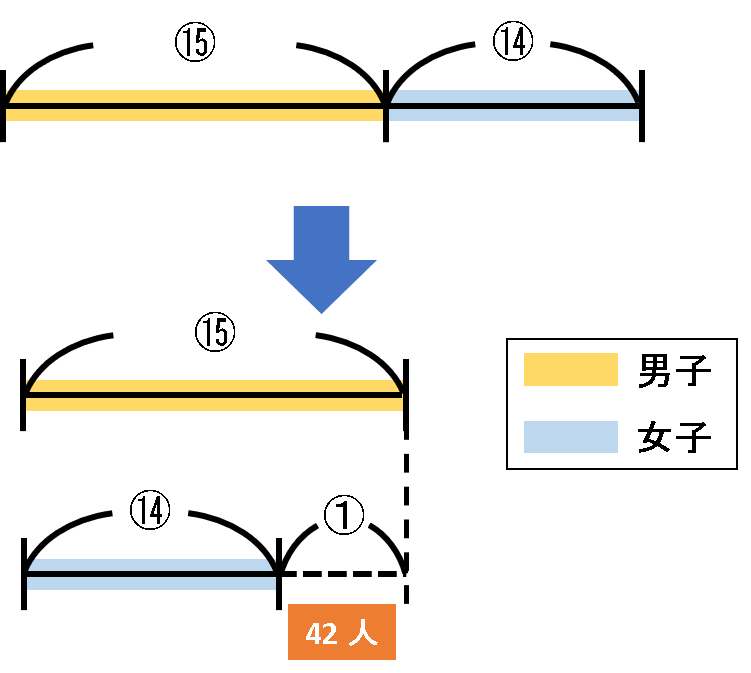
男女の比が15:14であることから、男子は①だけ多いことになります。
この①が42人と言うことになりますので、$ ⑮ = 42 \times 15 = 630 人, ⑭ = 42 \times 14 = 588 人 $と言うことになります。
よって全体の人数は$ 630 + 588 = 1218 人 $となります。
今回は、比を用いてその差から全体を求める問題を扱いました。
「相当算」の問題を解くうえでは、割合は、何に対してかを考える ことが大切です。
何を基準にして考える必要があるのかを理解するようにしましょう。
相当算はこちら↓








