基本問題 その2
中学受験を乗り越えるうえで避けられないのが算数です。
算数を苦手とする小学生は多いです。
そんな親御さんも含め小学生でも理解できるように、問題の解き方を基本から解説しています。
今まで複数回に分けて、「旅人算」「食塩水の問題」「仕事算」「過不足算」「相当算」の基本的な考え方について書いてきました。
今回は、「過不足算」でよくある「速度の違いによる到達時間」の問題の解き方について書いていきたいと思います。
速度の違いから時刻を決める
今回は、速度の違いによる到着時間の差から始業時刻を求める問題です。
＜基本問題2＞
ある生徒が、家を午前8時に出発し毎分90mの速さで歩くと、始業2分前に到着します。しかし、毎分72mの速さで歩くと、5分遅れてしまいます。学校までは何mありますか。また、学校の始業時刻は何時ですか。
基本的な考え方は、
<基礎問題1>～<基礎問題5>
<基礎問題6>～<基礎問題9>
と同じになります。
直接答えを知りたい方はこちら
速度の違いにより進む距離はどうなるか
まずは、下の例題を解いてみましょう。
＜例題1＞
予定時刻まで10分あります。毎分90mで歩いた時と毎分72mで歩いた時で進む距離はどれくらい変わりますか。
まず、速度のイメージについてです。
毎分90 mと72 mでは、1分で18 m変わります。
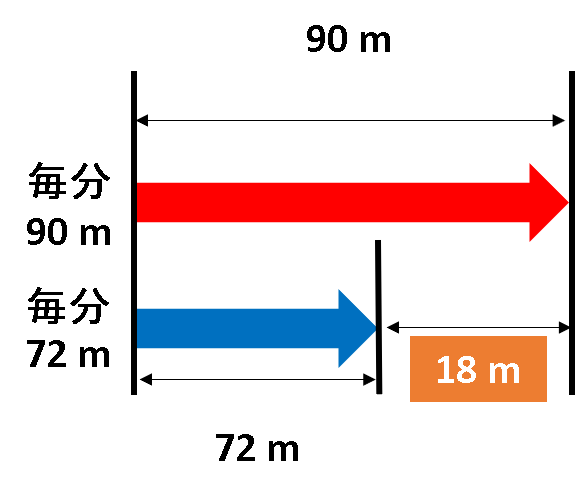
これが10分間経過すると、毎分90 m では$ 90 m \times 10分 =900 m$、毎分75 mでは $72 m \times 10分 = 720 m $進むことになります。
つまり、$ 900 m – 720 m = 180 m $になります。
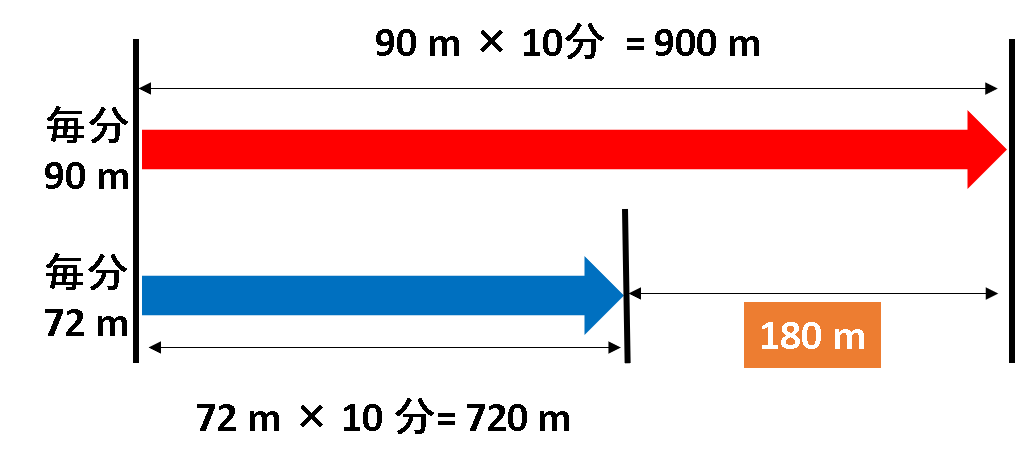
答えを出すだけであれば簡単な掛け算と引算で出すことができます。
ここで下の図を見て下さい。
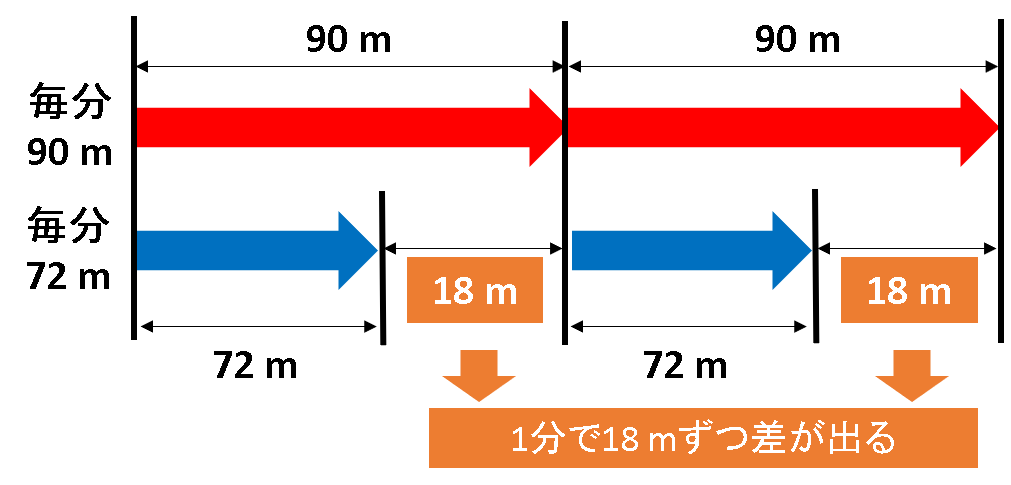
この図のように、90 mから72 mになることで1分で18 mずつ進む距離が変わると考えることが重要になります。
1分で18 mずつ変わるので、$18 m \times 10 分 = 180 m $変わるという考え方が過不足算の基本になります。
このように過不足算では、1つ当たりの数が変化すれば、変化した数×個数分必要な数が変化するということが大切な考えになります。
離れた距離から歩いた時間を求める
続いて、次の＜例題2＞を解いてみましょう。
＜例題2＞
同じ時刻に出発し毎分90mと毎分72 mの速さで歩くと、360 mの差が出来ました。何分歩きましたか。
＜例題2＞では、歩く早さの違いにより生じた距離の差から歩いた時間を求めます。
＜例題1＞で確認したように、毎分90 mと毎分72 mで歩い場合では1分で18 mの差が生じます。
よって、歩いた時間を□分とすると$ 18 m \times □ 分$差ができるということになります。
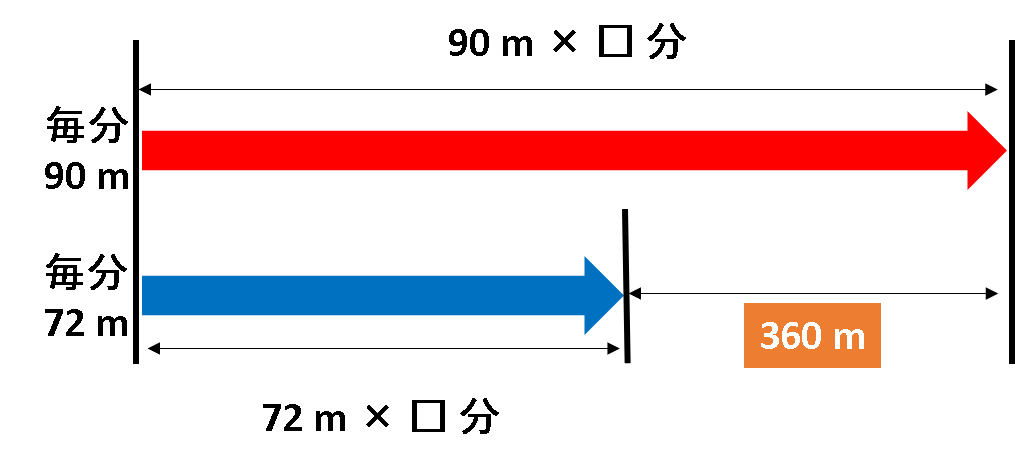
＜例題2＞では、360 m差ができていることからと$ 18 m \times □分 = 360 m$ということになり、$ □ = 360 \div 18 = 20 分$ということになります。
このように、離れた距離から歩いた時間を求めることが可能です。
予定時刻まで歩いた時の距離差を求める
＜例題3＞
同じ時刻に出発し、毎分90mの速さで歩くと予定時刻の4分前に、毎分72 mの速さで歩くと予定時刻の10分後に目的地へ到着しました。予定時刻まで歩いた場合、歩く距離は何 m変わりますか？
＜例題3＞では、歩く早さの違いにより到着時刻が変わっています。
まず毎分90 mで歩いた場合を考えてみましょう。
予定時刻の4分前に到着したので、後4分歩くことができます。
よって、$90 m \times 4 分 = 360 m $ 歩くことができます。
続いて、毎分72 m で歩いた場合を考えます。
予定時刻の10分後に到着したので、予定時刻からさらに10分間歩いて到着したということになります。
よって、予定時刻には、$72 m \times 10 分 = 720 m $手前にいたことになります。
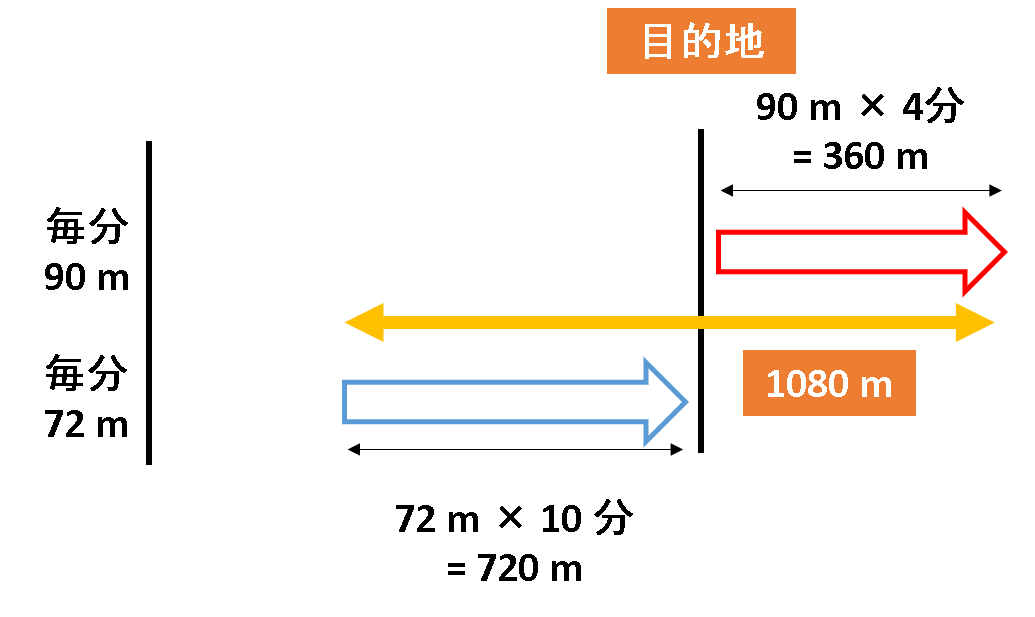
このことから、毎分90 mと毎分72 mでは、$360 m + 720 m = 1080 m $変わると言うことがわかります。
このように、到着時間の違いから予定時刻まで歩いた場合の距離差を求めることが可能です。
今回の問題の解説
＜基本問題2＞
ある生徒が、家を午前8時に出発し毎分90mの速さで歩くと、始業2分前に到着します。しかし、毎分72mの速さで歩くと、5分遅れてしまいます。学校までは何mありますか。また、学校の始業時刻は何時ですか。
今回の問題は、上で述べた＜例題1＞～＜例題3＞の考え方を基に解くことになります。
始業時刻まで歩いた時の距離差を求める
毎分90mの速さで歩くと、始業2分前に到着します。
このことから、始業時刻まで歩くと目的地からさらに$90 m \times 2 分 = 180 m $ 歩くことができます
一方、毎分72mの速さで歩くと始業時刻の5分後に到着することから、目的地より$72 m \times 5 分 = 360 m $ 手前にいることがわかります。
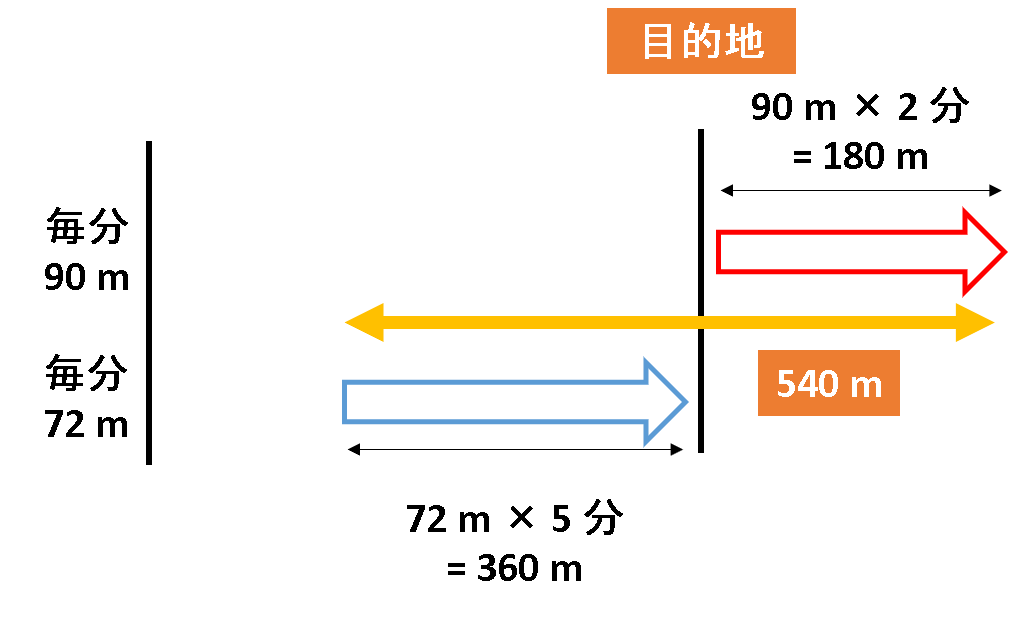
このことから、予定時刻まで歩いた時の差は、、$180 m + 360 m = 540 m $となります。
距離差から始業時刻までの時間を求める。
ここで下の図を見てください。
この図のように、90 mから72 mになることで1分で18 mずつ進む距離が変わります。
このことから、□分歩いたとすると歩いた時間を□分とすると$ 18 m \times □ 分$差ができるということになります。
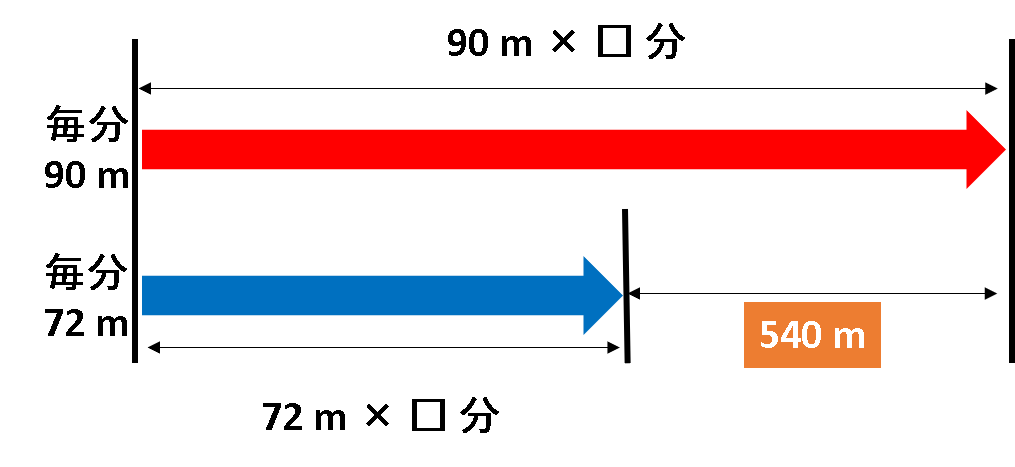
＜例題2＞では、540 m差ができていることからと$ 18 m \times □分 = 540 m$ということになり、$ □ = 540 \div 18 = 30 分$ということになります。
このことから、始業時刻の30分前に出発したことがわかります。
今回は午前8時に出発していますので、始業時刻は午前8時30分ということになります。
午前8時30分
過不足算の過去記事についてはこちら↓
