今回は、残った割合から全体をもとめる問題を考えていきしょう!
<この記事でわかること>
相当算の問題を解くのに必要な基礎的な考え方
『相当算』の基礎的な考え方 その2
中学受験を乗り越えるうえで避けられないのが算数です。
算数を苦手とする小学生は多いです。
そんな親御さんも含め小学生でも理解できるように、問題の解き方を基本から解説しています。
今まで複数回に分けて、「旅人算」「食塩水の問題」「仕事算」「過不足算」の基本的な考え方について書いてきました。
旅人算:同じ向きと逆向きに歩く違い
食塩水:濃度とは?百分率とは?
仕事算:1日の仕事量は?
過不足算:過不足算の基本について
相当算:相当算の基本について
今回は、「相当算」の基本的な考え方について書いていきたいと思います。
残りの割合から全体を求める問題
相当算を解くうえで大切なのが「割合」についてです。
割合とは、何に対してどれだけなのかを理解することがとても大切になります。
今回は全校生徒に対する割合から全体の人数を求める問題を考えていきます。
<基礎問題5>
学校に徒歩で通っている生徒は全体の$\frac{2}{5}$ , バスで通っている生徒は全体の $ \frac{5}{9} $ います。残りの電車で通っている人は全体のどれくらいですか。分数で答えなさい。
<基礎問題6>
学校に徒歩で通っている生徒は全体の $ \frac{2}{5} $, バスで通っている生徒は全体の $ \frac{4}{9} $ います。残りの電車で通っている人が14人います。生徒の人数は全部で何人ですか。
<基礎問題7>
ある学校の男子生徒の人数は全体の $ \frac{2}{5} $より14人多く、女子生徒の人数は全体の $ \frac{4}{9} $より6人多くなっています。生徒全体の人数を求めなさい。
では、<基礎問題5>から解いていきましょう。
全体に対する残りの割合
<基本問題5>は、「残りの人数の全体に対する割合を求める」問題です。
<基本問題5>
学校に徒歩で通っている生徒は全体の$\frac{2}{5}$ , バスで通っている生徒は全体の $ \frac{5}{9} $ います。残りの電車で通っている人は全体のどれくらいですか。分数で答えなさい。
線分図を書いて何がどこに当たるのかを考えてみましょう。
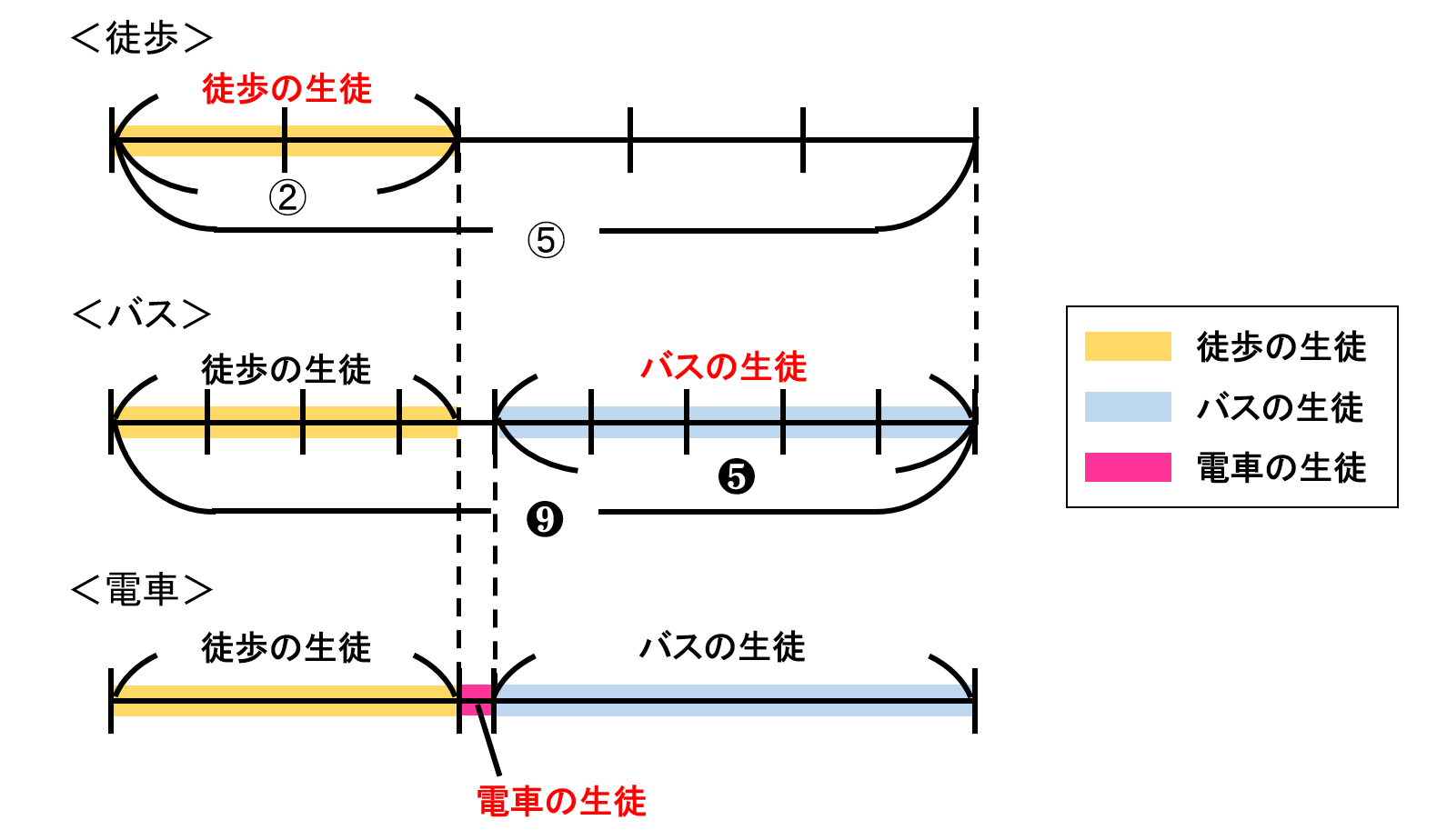
この図からもわかるように、$ \frac{2}{5} $とは全体を5としたうちの2つ分であり、$ \frac{5}{9} $とは全体を9としたうちの5つ分ということになります。
そして、残った部分(ピンク色)が電車の生徒ということになります。
しかし、このままでは電車の生徒が全体のどれくらいにあたるのかがわかりません。
ではどうしたらいいでしょうか。
方法は2つあります。
ではその方法について見ていきましょう。
方法1:全体の数を最小公倍数で揃える。
徒歩で通っている生徒は全体を5としたときの2つ分、バスで通っている生徒は全体を9としたときの5つ分です。
このままだと、全体の数が5と9で違っているので残った目盛りの数が分かりにくくなります。
そこで最小公倍数を使って全体の数を同じにします。
今回は、5と9ですので最小公倍数は45になります。
次の図を見てください。
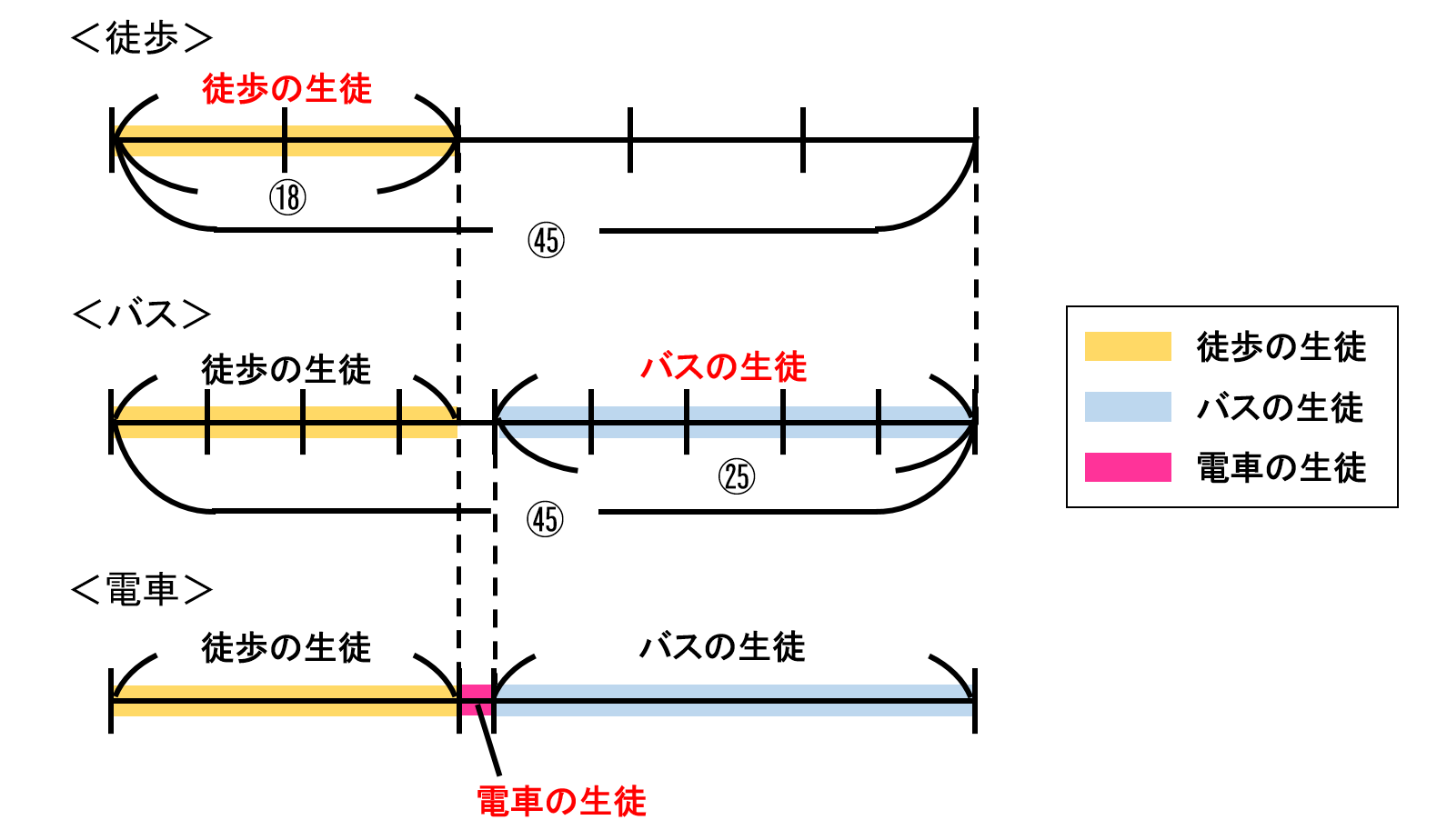
$ \frac{2}{5} = \frac{18}{45} $であり、$ \frac{5}{9} = \frac{25}{45} $です。
こうすると、全体を45としたときに徒歩の生徒は18であり、バスの生徒は25ということになります。
このことから、残りの電車で通う生徒は $ 45 -18 -25 = 2 $ということになります。
よって、電車で通う生徒の数は全体を45としたときの2ということになります。
このことから、<基礎問題5>の答えは $ \frac{2}{45} $ということになります。
では2つ目の方法にを見ていきましょう。
方法2:全体を1として考える。
2つ目の方法では、全体を1として考えます。
徒歩で通っている生徒は全体を5としたときの2つ分でした。
これを全体を1とするとどうなるでしょうか
次の図を見てください。
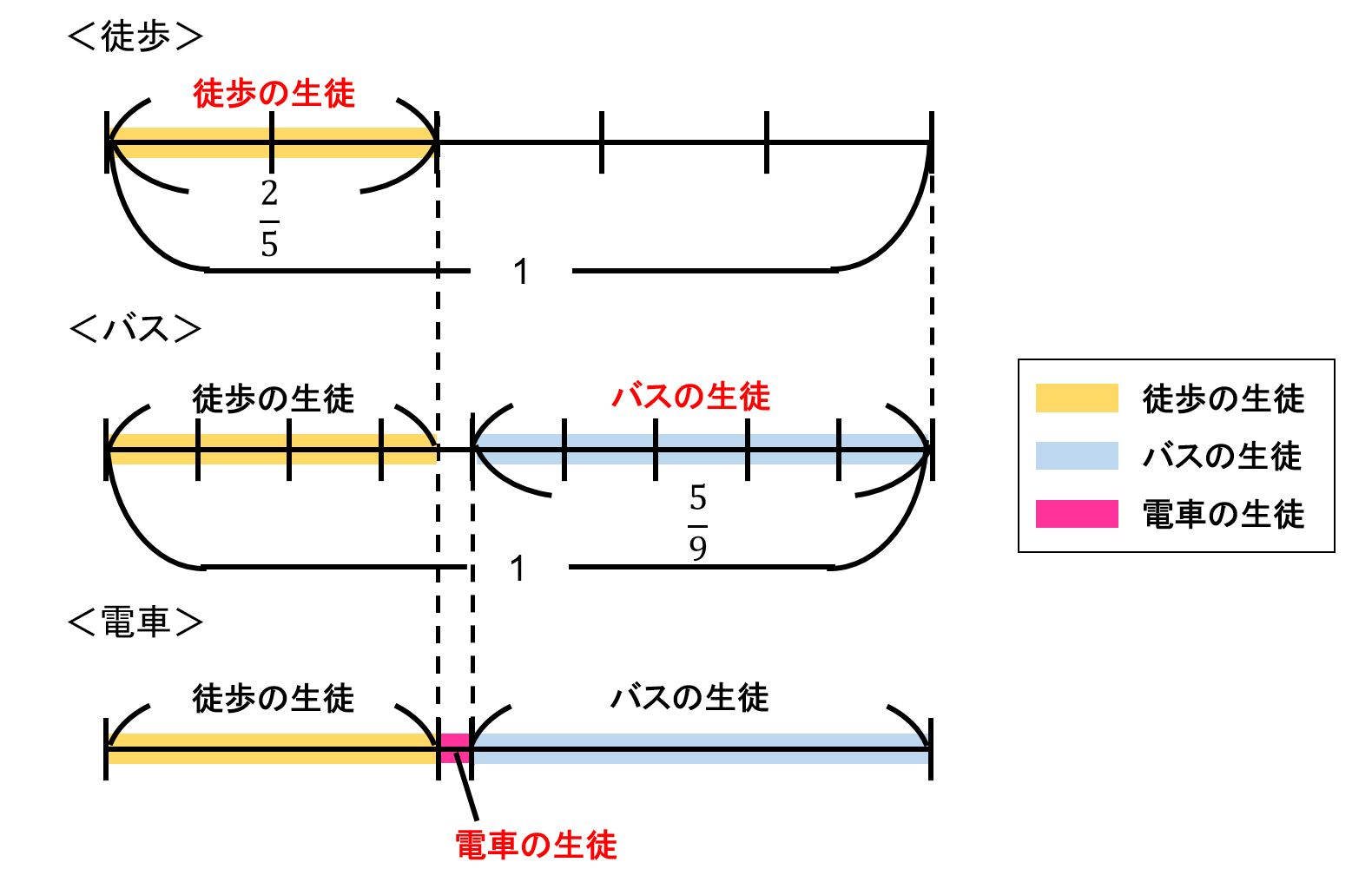
5だった全体を1とするので、5で割ることになります。
そうすると2は、$ 2 \div 5 = \frac{2}{5} $ということになります。
つまり、全体の$ \frac{2}{5} $ということは、全体を1としたときの$ \frac{2}{5} $という意味でもあります。
全体の$ \frac{△}{〇} $ = 全体を1としたうちの$ \frac{△}{〇} $
今回の問題では、全体を1とすると、徒歩の生徒は$ \frac{2}{5} $ バスの生徒は$ \frac{5}{9} $となります。
よって、電車で通っている生徒は $ 1 – \frac{2}{5} – \frac{5}{9} = \frac{45}{45} – \frac{18}{45} – \frac{25}{45} = \frac{2}{45} $ ということになります。
方法1, 2のどちらでも問題を解くことは可能ですが、可能であれば方法1で理解するようにしてください。
残りの割合から全体量を求める。
続いて、残りの割合から全体量を求める問題を考えていきましょう。
これは<基本問題2>と同じ考え方で解くことになります。
<基本問題6>
学校に徒歩で通っている生徒は全体の $ \frac{2}{5} $, バスで通っている生徒は全体の $ \frac{4}{9} $ います。残りの電車で通っている人が14人います。生徒の人数は全部で何人ですか。
相当算など割合を使って全体量を求めるうえで大事な考え方があります。
この考えを基に<基本問題6>を考えてみましょう。
今回は全体を求める問題で、電車で通っている生徒の人数があたえられています。
このことから、電車で通っている生徒の割合が求められれば全体の人数を求めることができると考えます。
では、電車で通っている生徒の割合を求めてみましょう。
前半は<基本問題5>と同じ内容ですので、電車で通っている生徒の割合は、$ \frac{2}{45} $となります。
ここまでくると、<基礎問題6>は次の問題と同じことになります。
<基礎問題6>
電車で通っている生徒は全体の $ \frac{2}{45} $で、人数は14人です。全体の生徒の人数を求めなさい。
これは<基礎問題2>と同じ考え方で解くことができます。
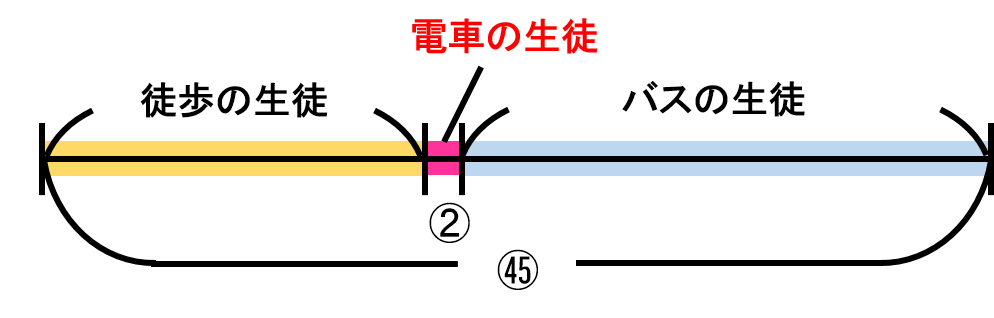
$ \frac{2}{45} $は、全体を45としたうちの2つ分なので、 $ ② = 14 $となり、$ ① = 7 $となります。
全体は㊺ですので、 $ ㊺ = 315 人$ ということになります。
では最後に<基礎問題7>を考えてみましょう。
余分な人数から全体の人数を求める。
<基礎問題7>
ある学校の男子生徒の人数は全体の $ \frac{2}{5} $より14人多く、女子生徒の人数は全体の $ \frac{4}{9} $より6人多くなっています。生徒全体の人数を求めなさい。
まずこれを図にしてみましょう。

図のように、上に実際の人数、下に割合を書きます。
この図を見ると、割合とそれに対する人数がどちらもわかっている所がありません。
ですので、このままでは解けません。
この問題を解くためには、3つのことが考えられます。
2:$ \frac{4}{9} $にあたる人数を求める
3:14人もしくは6人にあたる割合を求める
この中で、男子生徒と女子生徒の人数がどちらもわからないので1, 2を求めることはできません。
そこで、3について考えていきましょう。
今回は、14人もしくは6人にあたる割合は出すのは難しそうですが、それらを足した20人にあたる割合は出せそうです。
では、70人にあたる割合はいくらでしょうか。
全体1 から$ \frac{2}{5} $と$ \frac{4}{9} $を引いた値が70人にあたる割合になります。
よって、$ 1 – \frac{2}{5} – \frac{5}{9} = \frac{45}{45} – \frac{18}{45} – \frac{25}{45} = \frac{2}{45} $ となります。
ここまでくると、<基本問題7>は次の問題と同じことになります。
<基礎問題7>
全体の $ \frac{2}{45} $にあたる人数は20人です。全体の生徒の人数を求めなさい。
これは<基礎問題2>と同じ考え方で解くことができます。
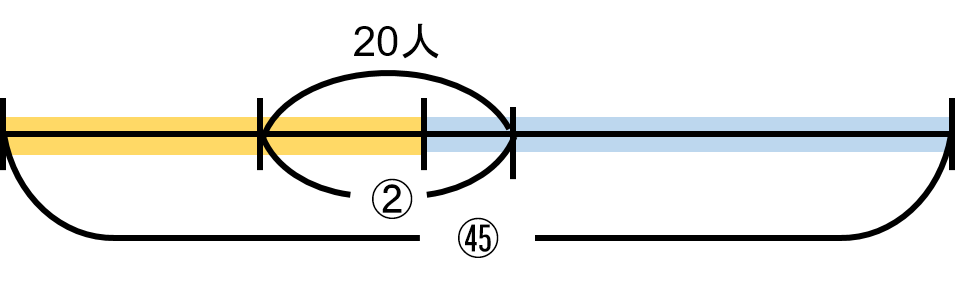
$ \frac{2}{45} $は、全体を45としたうちの2つ分なので、 $ ② = 20 $となり、$ ① = 10 $となります。
全体は㊺ですので、 $ ㊺ = 450 人$ ということになります。
今回は、前回とは少し違った相当算の基本的な問題を扱いました。
「相当算」のような割合を使った問題を解くうえではこの考え方がとても大切です。
次回は、この考え方を基に標準的な問題を考えていきたいと思います。






