[usemath]
『仕事算』の標準問題の解き方 その1
中学受験を乗り越えるうえで避けられないのが算数です。
算数を苦手とする小学生は多いです。
そんな親御さんも含め小学生でも理解できるように、問題の解き方を基本から解説しています。
今まで複数回に分けて、「旅人算」「食塩水の問題」について基本的な考え方について書きました。
旅人算:同じ向きと逆向きに歩く違い
食塩水:濃度とは?百分率とは?
仕事算:1日の仕事量は?
過不足算:過不足算の基本について
相当算:相当算の基本について
「仕事算」については、基本問題を使って基本的な考え方について書きました。
今回は、その基本的な考え方を用いて標準的な問題を解いてみましょう。
複数人が分担して働いた場合にかかる時間を求める。
今回は、A, B, Cの3人がそれぞれバラバラに働いた場合にかかる時間を求める問題を考えてみましょう。
<標準問題1>
ある仕事をするのに、Aさん1人で行うと24日、Bさん1人で行うと30日、A, B, Cの3人で行うと8日で終わります。この仕事を、AさんとBさん2人で6日働いた後、AさんとCさん2人で仕事をしました。仕事を始めてから終わるまでに何日かかりましたか。
どうやって解いていくかを考える癖をつける
まずこの問題を解く前に、親御さんにお願いしたいことがあります。
文章問題を解いていく上で、小学生がよくやってしまうのは「いきなり答えを出そうととする」ことです。
いくら説明をしても、いざ問題を解こうとすると答えをいきなり出そうとして、書いてある数字を足したりかけたりしようとします。
小学生が1人で解くためには、文章問題をしっかり読んで理解する癖をつけることが大切です。
ですので、親御さんがお子さんと一緒に問題を解く際に「この問題はこれから解けばいい」と教えてしまうのではなく、「どういった順番で考えていけばいいか」を一緒に考えてあげるようにしてください。
どう考えればいいか。
では、この問題をどう解けばいいか考えていきましょう。
まず「仕事算」の問題を解くうえで大切な考え方が次になります。
- 全体の仕事量を1として考える
- 仕事をする日数を出すには、1日の仕事量が必要
- する仕事量 ÷ 1日の仕事量 = かかる日数
このことを基に<標準問題1>を考えていきましょう。
Aさん、Cさんが一緒に何日仕事をしたかを求める
<標準問題1>は、「仕事を始めてから終わるまでに何日かかるか」を求める問題になります。
AさんとBさん2人で6日働いたと書いてあるので、AさんとCさんが一緒に何日仕事したかを求めれば答えが出ることになります。
- ① AさんとCさんが一緒に何日仕事したかを求める。
では、AさんとCさんが一緒に何日仕事したかを求めるにはどうしたらいいでしょうか?
かかる日数は、する仕事量 ÷ 1日の仕事量で出すことができます。
このことから、AさんとCさんが一緒に何日仕事したかを求めるには、「AさんとCさんが一緒にする仕事量」「AさんとCさんが一緒に仕事をしたときの1日の仕事量」とが必要ということになります。
- ② AさんとCさんが一緒にする仕事量を求める。
- ③ AさんとCさんが一緒に仕事をしたときの1日の仕事量を求める
AさんとCさんが2人で一緒にする仕事量を求める。
まず、② AさんとCさんが一緒にする仕事量を求めるにはどうしたらいいかを考えてみましょう。
AさんとCさんが一緒にする仕事量は、「AさんとBさん2人が一緒に6日間した残りの仕事量」になります。
つまり、全体の仕事量からAさんとBさんが一緒にした仕事量を引いた量が、AさんとCさんが一緒にする仕事量になります。
AさんとBさんは一緒に6日間働いたと書いてあるので、④ AさんとBさんが一緒に仕事をしたときの1日の仕事量を求めれば、AさんとCさんがする仕事量を出すことができます
- ④ AさんとBさんが一緒に仕事をしたときの1日の仕事量を求める
AさんとCさんが一緒に仕事をしたときの1日の仕事量を求める
続いて、② AさんとCさんが一緒に仕事をしたときの1日の仕事量を求めるにはどうしたらいいかを考えてみましょう。
② AさんとCさんが一緒に仕事をしたときの1日の仕事量は、Aさん、Cさんそれぞれが1人で1日でする仕事量の足し算で出すことができます。
今回は、「Aさん, Bさんそれぞれが1人で行った時の日数」「A, B, Cさん3人で行った時の日数」があたえられています。
Aさんが1日でする仕事量は、「Aさんが1人で行った時の日数」から求めることが出来ます。
しかし、「Cさんが1人で行った時の日数」はあたえられていません。
では、Cさんが1人で1日でする仕事量はどう出せばいいでしょうか。
ここで、<基礎問題6>を思い出してください。
Cさん1人が1日でする仕事量は、「3人一緒に1日でする仕事量」から「A, B2人が一緒に1日でする仕事量」を引くことで求めることができます。
「A, B2人が一緒に1日でする仕事量」は、④のことですので必要なのは「3人一緒に1日でする仕事量」になります。
- ⑤ A, B, C3人で1日にする仕事量を求める。
ここまでの事をまとめると以下のようになります。
- <考えの流れ>
① AさんとCさんが何日仕事をしたか
② AさんとCさんがする仕事量はどれだけか
③ AさんとCさんは2人では1日どれだけ仕事をするか
④ AさんとBさんは2人では1日どれだけ仕事をするか
⑤ A, B, Cさん3人で1日にする仕事量はどれだけか
今回は、この6つのことを求めることができれば答えを求めることができることがわかりました。
ではどの順番で解いていくかを考えてみましょう。
解く順番を考える。
先ほど考えたことをどの順番で求めていくかを考えます。
基本的には先ほど考えた<考えの流れ>の逆に解いていくことになります。
- <解く順番>
① A, B, Cさん3人で1日にする仕事量はどれだけか
② AさんとBさん2人では1日どれだけ仕事をするか
③ AさんとCさん2人では1日どれだけ仕事をするか
④ AさんとCさんがする仕事量はどれだけか
⑤ AさんとCさんが何日仕事をしたか
ではこの順番で<標準問題1>を解いていきましょう。
<標準問題1>
ある仕事をするのに、Aさん1人で行うと24日、Bさん1人で行うと30日、A, B, Cの3人で行うと8日で終わります。この仕事を、AさんとBさん2人で6日働いた後、AさんとCさん2人で仕事をしました。仕事を始めてから終わるまでに何日かかりましたか。
① A, B, Cさん3人で1日にする仕事量はどれだけか
「A, B, Cさん3人で行った時の日数」があたえられていますので<基本問題1>と同じ考え方で求めることが出来ます。
下の図を見てください。
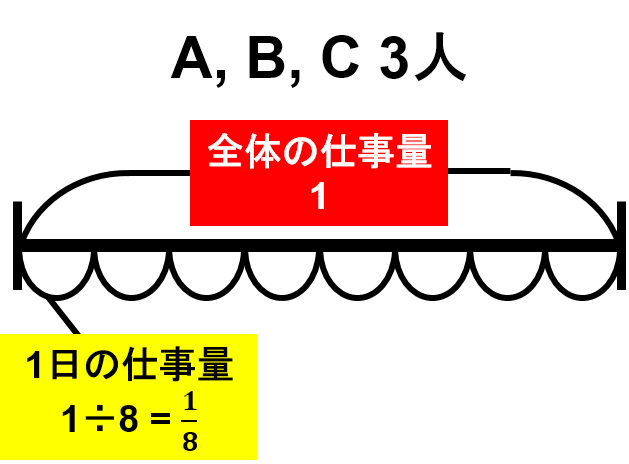
A, B, Cの3人で行うと8日で終わるので、$ 1 \div 8 = \frac{1}{8} $が3人で1日でする仕事量になります。
- A, B, C3人が1日でする仕事量は、$ \frac{1}{8} $
② AさんとBさん2人では1日どれだけ仕事をするか
「Aさん, Bさんそれぞれが1人で行った時の日数」から、「Aさん、Bさん2人で1日にする仕事量」を求めます。
これは、<基本問題2>と同じ考えになります。
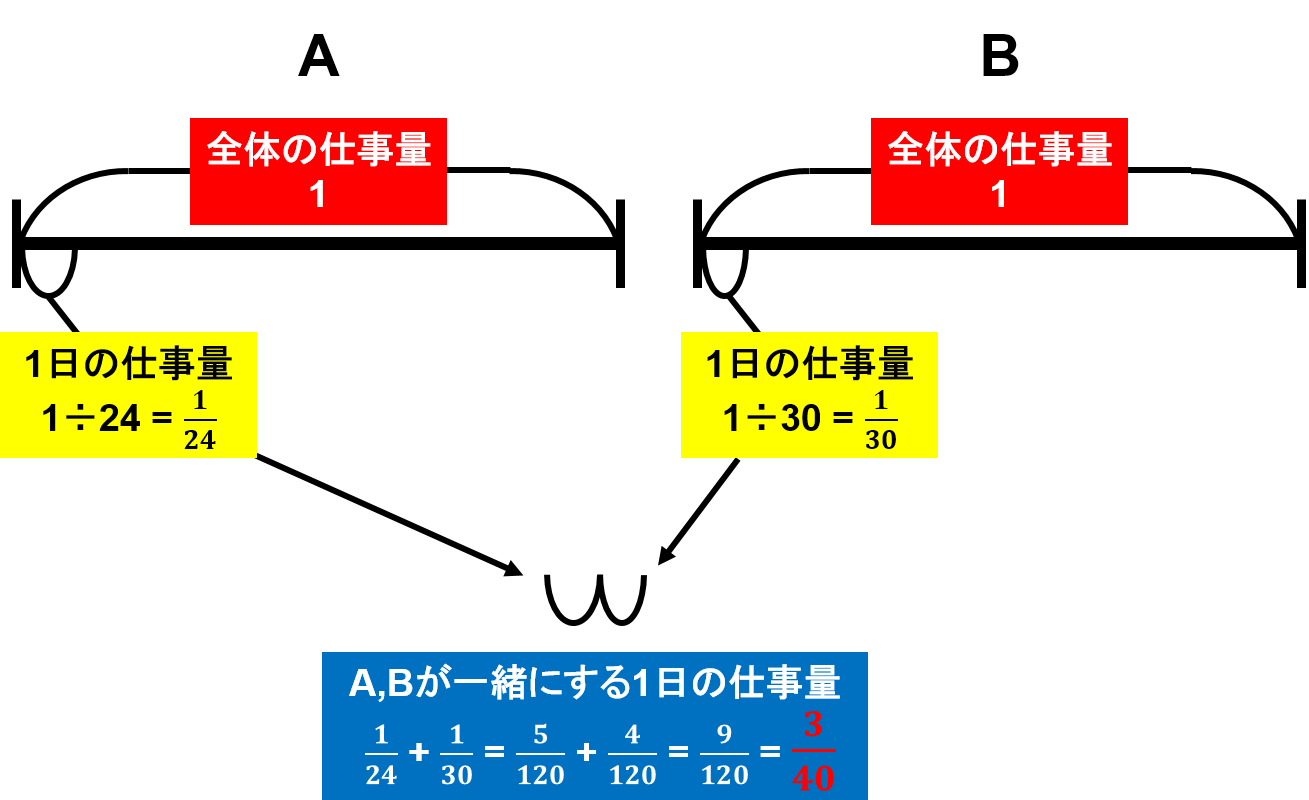
まず、Aさん、Bさんそれぞれが1日でする仕事量を求めます。
Aさん1人では24日で終わるので、Aさんが1日でする仕事量は$ 1 \div 24 = \frac{1}{24} $ということになります。
同様に、Bさんが1日でする仕事量は $ 1 \div 30 = \frac{1}{30} $になります。
よって、「Aさん、Bさん2人で1日にする仕事量」は $ \frac{1}{24} + \frac{1}{30} = \frac{5}{120} + \frac{4}{120} = \frac{9}{120} =\frac{3}{40} $ ということになります。
- A, B2人で1日にする仕事量は、$ \frac{3}{40} $
③ AさんとCさん2人では1日どれだけ仕事をするか
「Aさん, Cさん2人で1日にする仕事量」は、「Aさん、Cさんそれぞれが1日にする仕事量」から出すことができます。
②でAさんが1日にする仕事量は$ \frac{1}{24} $ と求めていますのでCさんが1日でする仕事量を求めます。
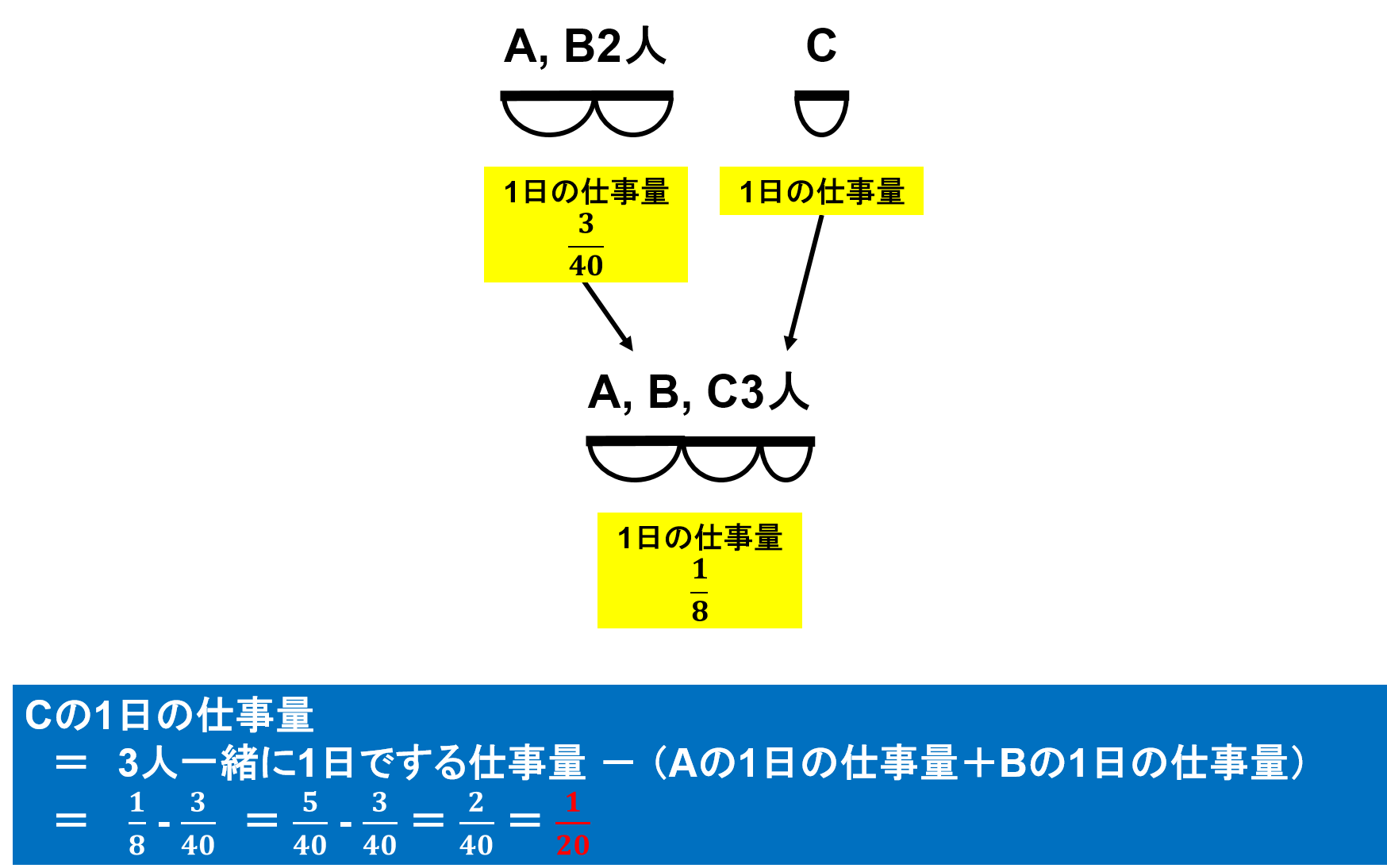
考え方のところにも書きましたが、今回は<基礎問題6>と同じように「Cさんが1日でする仕事量」を「3人一緒に1日でする仕事量」から「A, B2人が一緒に1日でする仕事量」を引くことで出します。
①②で、「3人一緒に1日でする仕事量」は$ \frac{1}{8} $、「A, B2人が一緒に1日でする仕事量」は $ \frac{3}{40} $と求めています。
よって、「Cさんが1日でする仕事量」は $ \frac{1}{8} – \frac{3}{40} = \frac{5}{40} – \frac{3}{40} = \frac{2}{40} = \frac{1}{20} $ということになります。
このことから、「Aさん, Cさん2人で1日にする仕事量」は$ \frac{1}{24} + \frac{1}{20} = \frac{5}{120} + \frac{6}{120} = \frac{11}{120} $ということになります。
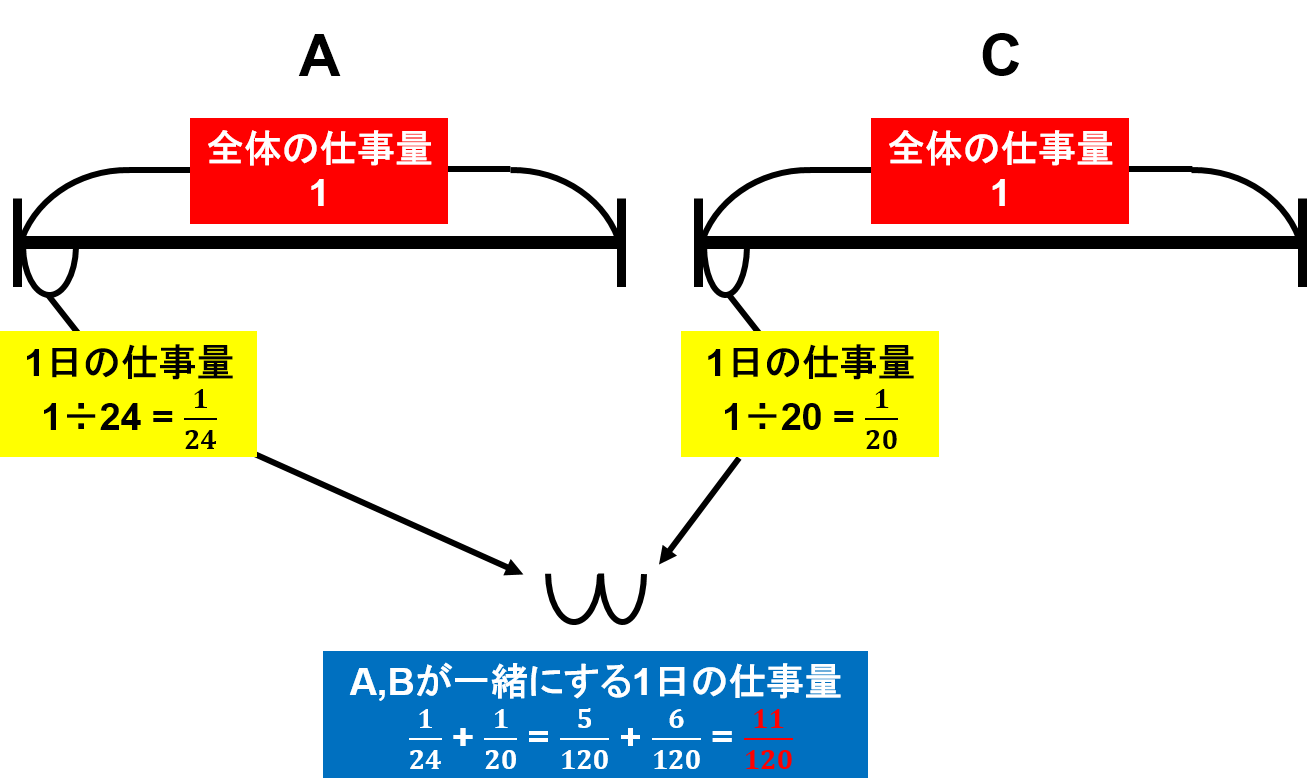
- A, C2人が1日でする仕事量は、$ \frac{11}{120} $
④ AさんとCさんがする仕事量はどれだけか
AさんとCさんがする仕事量は、AさんとBさんが6日間でして残った量になります。

②でA, B2人で1日にする仕事量は$ \frac{3}{40} $と求めていますので6日間でする仕事量は、 $ \frac{3}{40} \times 6 = \frac{18}{40} = \frac{9}{20} $になります。
AさんとCさんは残った仕事をすることになるので、$ 1 – \frac{9}{20} = \frac{20}{20} – \frac{9}{20} = \frac{11}{20} $ が2人がする仕事になります。
- A, C2人が1日でする仕事量は、$ \frac{11}{20} $
⑤ AさんとCさんが何日仕事をしたか
③④で、「A, C2人が1日でする仕事量は$ \frac{11}{120} $」「A, C2人が1日でする仕事量は、$ \frac{11}{20} $」と求まりました。
かかる日数はする仕事量 ÷ 1日の仕事量で求めることができるので、A, C2人でした仕事の日数は $ \frac{11}{20} \div \frac{11}{120} = \frac{11}{20} \times \frac{120}{11} = 6日 $ ということになります。
- A, C2人が仕事した日数は、6日
最終的に求めるのは何か。
ここまでくれば、答えは出たようなものです。
しかし、ここで油断してはいけません。
今回求めないといけないのは、「仕事を始めてから終わるまでの時間」です。
A, B2人で6日間仕事をした後に、A, C2人で6日間仕事をします。
よって、求める答えは$ 6 + 6 = 12日間 $になります。
この問題を6日と答える小学生は本当に多いです。
中学受験は解答のみしか書かないことが多いです。
ここまで出していても、6日と答えてしまえば0点です。
最後に何を求めないといけなかったのかを確認する癖をつけましょう。
今回は、「仕事算」の標準問題について考えました。
文章題を次の順番で解く癖を付けてください。
- 答えを出すために何を出す必要があるかを考える
- 考えた事をどの順番で解くかを考える
- 最後に何を答えるのかを確認する
次回以降も、仕事算の標準~応用問題を解いていきたいと思います。



