[usemath]
『仕事算』の基本的な考え方 その2
中学受験を乗り越えるうえで避けられないのが算数です。
算数を苦手とする小学生は多いです。
そんな親御さんも含め小学生でも理解できるように、問題の解き方を基本から解説しています。
今まで複数回に分けて、「旅人算」「食塩水の問題」「仕事算」「過不足算」について書いてきました。
旅人算:同じ向きと逆向きに歩く違い
食塩水:濃度とは?百分率とは?
仕事算:1日の仕事量は?
過不足算:過不足算の基本について
相当算:相当算の基本について
以前「仕事算」の基本的な考え方について書きました。
今回はその続きになります。
今後標準的な問題を解くうえ今回の考え方も重要ですのでしっかり理解しておきましょう。
複数人の仕事量から1人の仕事量を求める。
今回は複数人で終わる日数から1人で終わらせることのできる日数を求める問題について考えていきます。
<基本問題5>
A, Bが2人で仕事をすると2日で終わる仕事があります。この仕事をAさんだけで行うと6日かかります。この仕事をBさんだけで行うと何日かかりますか。
<基本問題6>
ある仕事をするのに、Aだけでは12日、Bだけでは15日で、A, B, Cの3人ですると4日で終わります。この仕事をCだけで行うと何日で終わりますか。
では、<基礎問題6>から解いていきましょう。
2人の仕事量から1人の仕事量を求める。
前回も書きましたが、仕事算を考えるうえで必ず必要になるのが「1日の仕事量」です。
<基礎問題5>では、A, Bの2人での仕事量からBさん1人の仕事量を求めます。
<基本問題5>
A, Bが2人で仕事をすると2日で終わる仕事があります。この仕事をAさんだけで行うと6日かかります。この仕事をBさんだけで行うと何日かかりますか。
この問題もまず 全体の仕事量を1として考える ことから始めます。
下の図を見てください。
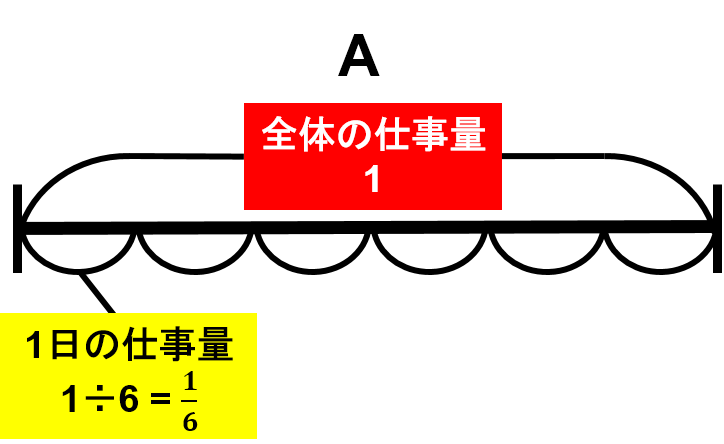
Aさんは、6日間かけてすべての仕事を終わらせることができます。
毎日同じ量だけ仕事をするので、1日で終わらすことのできる仕事量は $ 1 \div6 = \frac{1}{6} $ということになります。
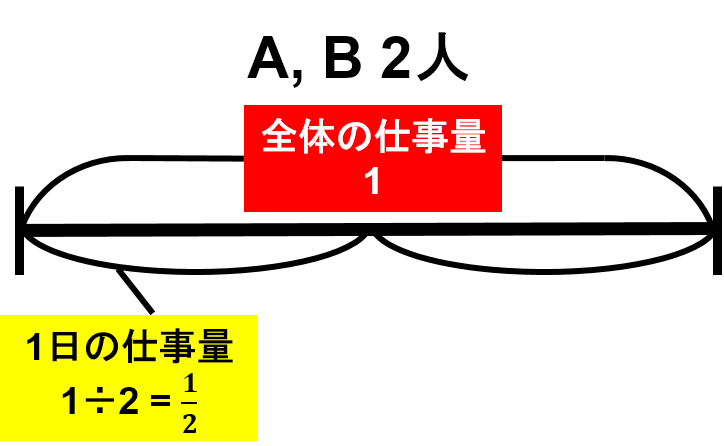
一方、A, Bさん2人が仕事をすると2日で終わらせることができます。
このことから、2人では1日で$1 \div 2 = \frac{1}{2} $ということになります。
ここで、次の図を見てください。
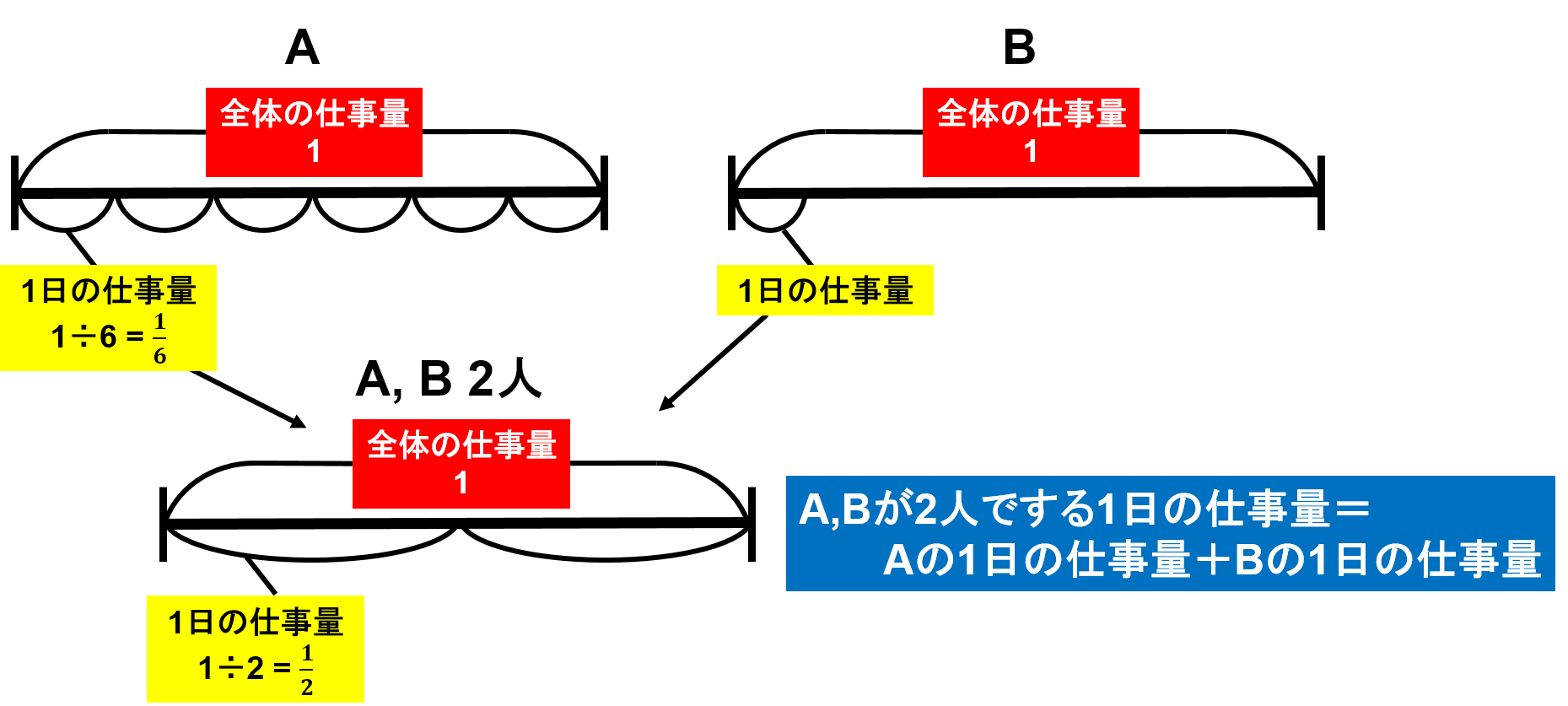
A, Bさんそれぞれが1日でする仕事量を足し合わせたものが、2人で1日でする仕事量になります。
ですので、Bさんが1日でする仕事量は、2人一緒に1日でする仕事量からAさんが1日でする仕事量を引いた量になります。
よって、$ \frac{1}{2} – \frac{1}{6} = \frac{1}{3} $ がBさんが1日でする仕事量になります。
ここまで来ると する仕事量 ÷ 1日の仕事量 = かかる日数から答えが出せます。
今回はすべての仕事を終わらせるまでの日数ですので、$ 1 \div \frac{1}{3} = 1 \times 3 = 3日 $が答えになります。
では、続いて<基礎問題6>を考えてみましょう。
3人の仕事量から1人の仕事量を求める。
先ほどは、2人でする仕事量から1人でする仕事量を求めました。
続いて考える問題は、3人でする仕事量から1人でかかる日数を求めます。
基本的な考え方は<基礎問題5>と同じです。
この問題も、全体の仕事量を1として考えます。
<基本問題6>
ある仕事をするのに、Aだけでは12日、Bだけでは15日で、A, B, Cの3人ですると4日で終わります。この仕事をCだけで行うと何日で終わりますか。
Aさんが1人でこの仕事を仕上げようと思うと12日かかります。
ですので、Aさんが1日でできる仕事量は$ 1 \div 12 = \frac{1}{12} $ということになります。
同じように考えて、Bさんが1日でする仕事量は$ 1 \div 15 = \frac{1}{15} $ということになります。
また、A, B, Cの3人で一緒にしたときに1日でする仕事量は $1 \div 4 = \frac{1}{4} $になります。
次の図を見てください。
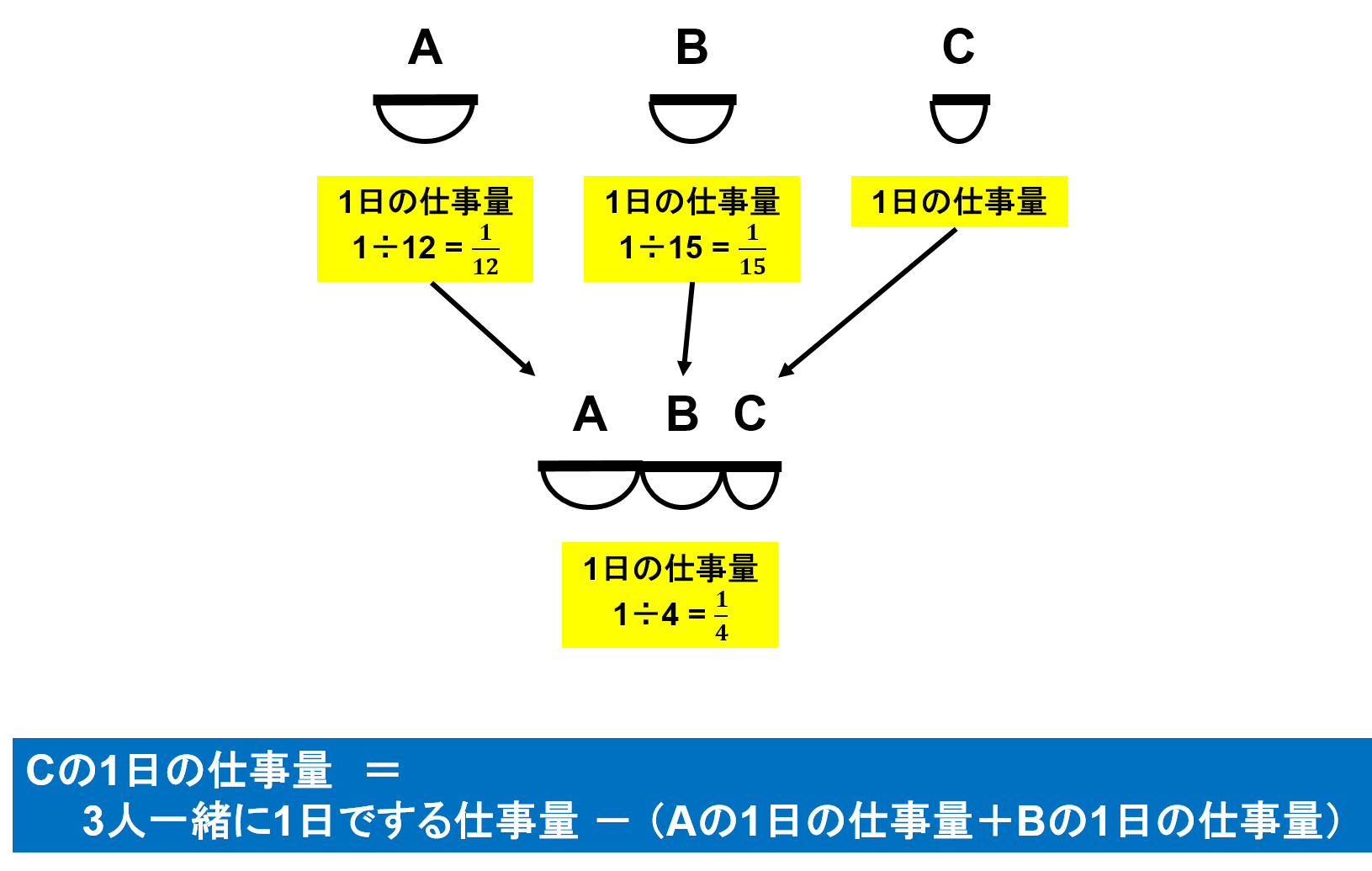
A, B, Cさんそれぞれが1日でする仕事量を足し合わせたものが、3人で1日でする仕事量になります。
ですので、Cさんが1日でする仕事量は、3人一緒に1日でする仕事量からAさんとBさん2人が1日でする仕事量を引いた量になります。
そこでまず、AさんとBさん2人が1日でする仕事量をもとめます。
Aさんは1日で$\frac{1}{12}$、Bさんは1日で$\frac{1}{15}$仕事を終わらせることができます。
このことから、A, B2人で$ \frac{1}{12} + \frac{1}{15} = \frac{5}{60} + \frac{4}{60} = \frac{9}{60} = \frac{3}{20} $となります。
よって、Cさんが1日でする仕事量は、$ \frac{1}{4} – \frac{3}{20} = \frac{5}{20} – \frac{3}{20} = \frac{2}{20} = \frac{1}{20} $となります。
する仕事量 ÷ 1日の仕事量 = かかる日数からかかる日数は、$ 1 \div \frac{1}{20} = 1 \times 20 = 20日 $
となります。
今回は2人ないし3人の仕事量から1人の仕事量を求める問題を扱いました。
次回は、<基礎問題1>から<基礎問題6>の考え方を用いて標準~応用問題を解いていきたいと思います。


