『相当算』
中学受験を乗り越えるうえで避けられないのが算数です。
算数を苦手とする小学生は多いです。
そんな親御さんも含め小学生でも理解できるように、問題の解き方を基本から解説しています。
今まで複数回に分けて、「旅人算」「食塩水の問題」「仕事算」「過不足算」の基本的な考え方について書いてきました。
旅人算:同じ向きと逆向きに歩く違い
食塩水:濃度とは?百分率とは?
仕事算:1日の仕事量は?
過不足算:過不足算の基本について
今回は、「相当算」の基本的な考え方について書いていきたいと思います。
相当算の基礎的な考え方:割合
相当算を解くうえで大切なのが「割合」についてです。
割合とは、何に対してどれだけなのかを理解することがとても大切になります。
相当算は、線分図を書いて何がどこに当たるのかを考えて解いていきます。
<基礎問題1>
ある本を全体の$ \frac{3}{5} $だけ読むと、28ページ残りました。全部で何ページありましたか。
<基礎問題2>
ある本を1日目に28ページ読み、2日目に残りの$ \frac{2}{5} $読んだところ30ページ残りました。全部で何ページありましたか。
<基礎問題3>
ある本を1日目に全体の$ \frac{1}{5} $ だけ読み、2日目に残りの$ \frac{1}{3} $ だけ読むと48ページ残りました。全部で何ページありましたか。
<基礎問題4>
ある本を1日目に全体の$ \frac{1}{3} $だけ読み、2日目に28ページだけ読みました。3日目に残りの$ \frac{5}{8}だけ読んだところ、読み残したページが24ページありました。この本は全体で何ページありますか?
では、<基礎問題1>から解いていきましょう。
全体に対する割合
<基礎問題1>は全体に対する割合を用いて解く問題です。
ある本を全体の$ \frac{3}{5} $だけ読むと、28ページ残りました。全部で何ページありましたか。
全体の$ \frac{3}{5} $とはどういう意味でしょうか。
下の図を見てください。
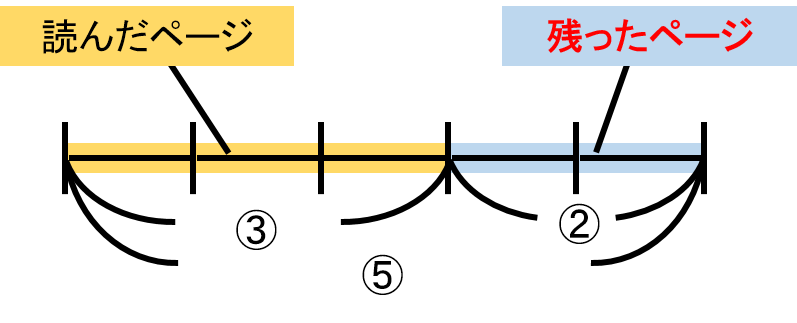
この図からもわかるように、$ \frac{3}{5} $とは全体を5としたうちの3目盛り分が読んだページということになります。
3目盛り分読んだので、残ったのは2目盛り分ということになります。
今回は28ページ残ったので、2目盛りにあたるのが28ページになります。
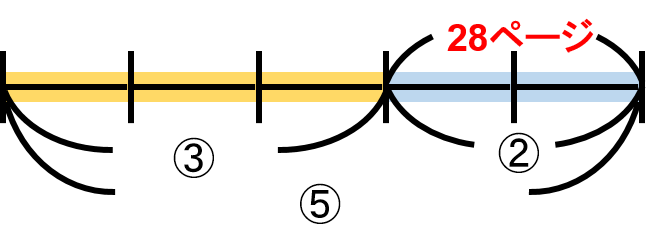
上の図から、$ ② = 28 $となり、$ ① = 14 $ということになります。
よって、全体を表す$ ⑤ = 70 $となり、この本の全ページ数は70ページということになります。
では、続いて<基礎問題2>について考えてみましょう。
残った部分に対する割合
<基礎問題2>は、<基礎問題1>と異なり残ったページに対する割合を用います。
ある本を1日目に28ページ読み、2日目に残りの$ \frac{2}{5} $読んだところ30ページ残りました。全部で何ページありましたか。
1日目に28ページ読み、2日目は残ったページの$ \frac{2}{5} $を読んだと書いてあります。
先ほどは本全体に対する割合でしたが、今回は残ったページに対する割合です。
下の図を見てください。
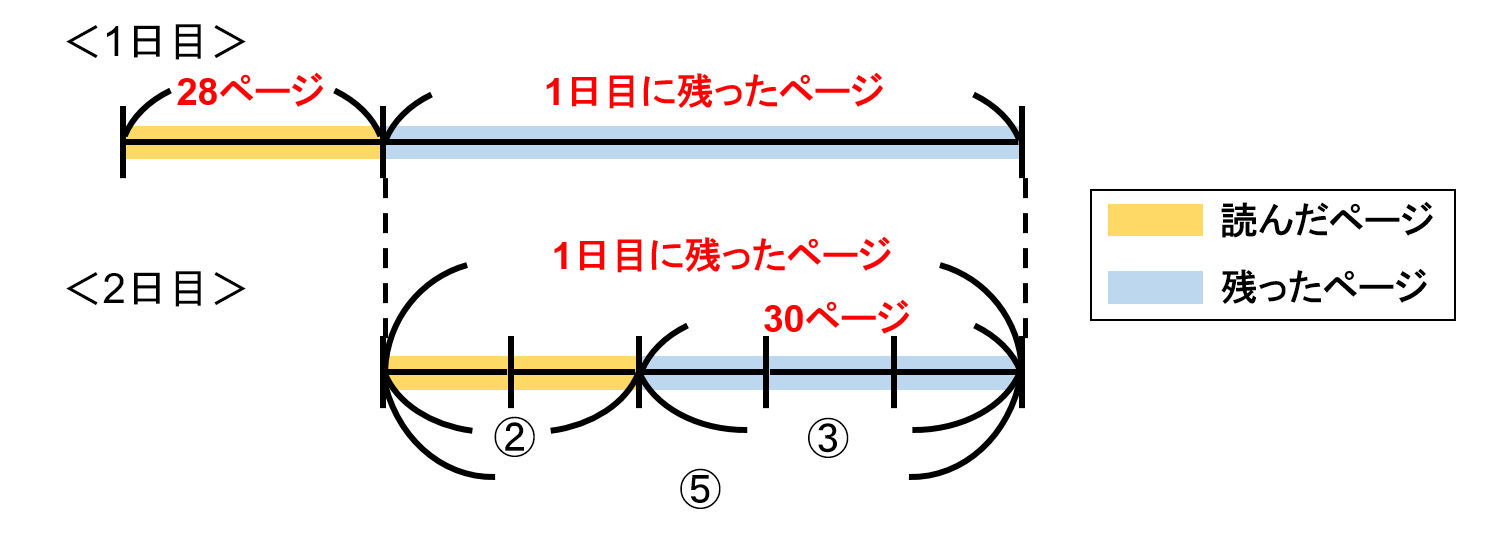
残ったページの$ \frac{2}{5} $なので、残ったページ全体を5としたときの2目盛り分を2日目に読んだことになります。
2目盛り分読んだので、3目盛り分が残った30ページということになります。
ここからは<基礎問題1>と同じようにして、$③ = 30 ページ$から$ ① = 10 ページ $となるので、1日目に残っていたのは$ ⑤ = 50 ページ $ということになります。
1日目には28 ページ読んでいたので、この本は全部で $ 28 + 50 = 78ページ $あったということになります。
<基礎問題1><基礎問題2>からわかるように、割合を考える時は何に対してなのかを考えることが大切です。
全体に対する割合と残った部分に対する割合
<基礎問題3>では、全体に対する割合と残った部分に対する割合を組み合わせた問題を扱います。
ある本を1日目に全体の$ \frac{1}{5} $ だけ読み、2日目に残りの$ \frac{1}{3} $ だけ読むと48ページ残りました。全部で何ページありましたか。
まず、下の図のように<基礎問題1>と同じように考えます。
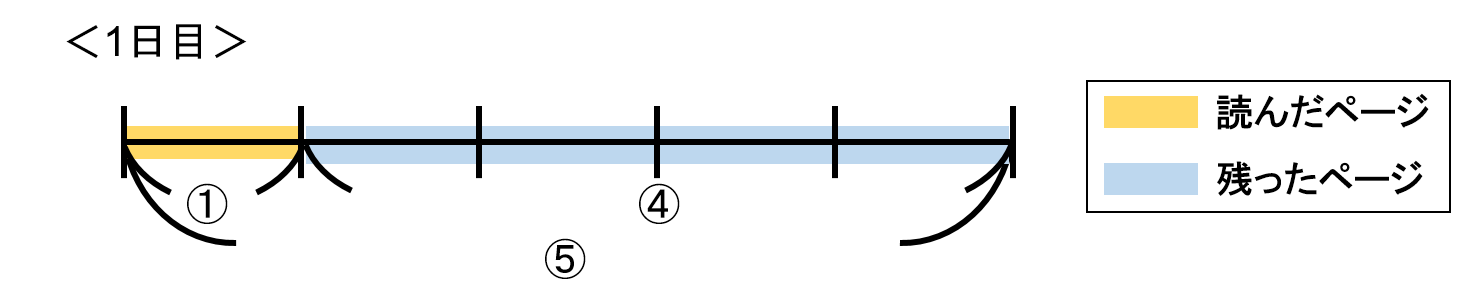
1日目は全体の$ \frac{1}{5} $ を読んだので、全体を5としたうちの1目盛り分を読み、残ったのは4目盛り分ということになります。
続いてこの残った部分に対する割合を考えます。
2日目は、この残ったページの$ \frac{1}{3} $を読んだので次の図の様になります。
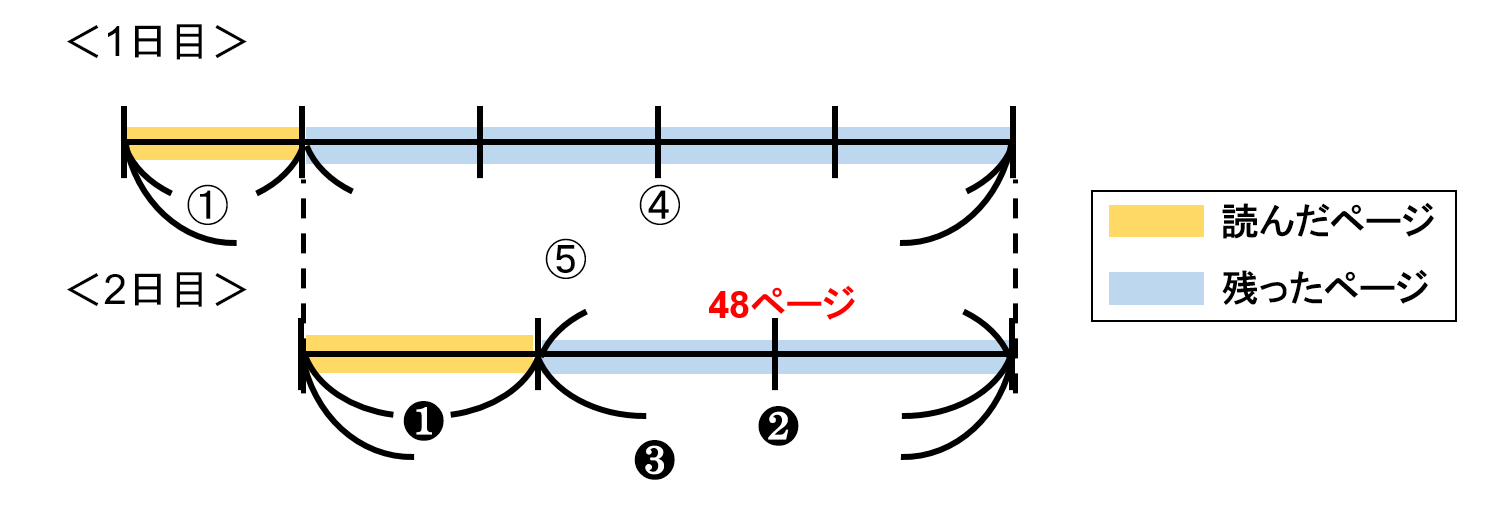
2日目は、残ったページ全体を3としたときの1目盛り分を読みました。そして残ったのが2目盛り分になります。
この2目盛り分にあたるのが48ページになります。
よって、$ ❷ = 48 ページ $となり、$ ❶ = 24 ページ $ということになります。
残ったページ全体は $ ❸ $ なので、1日目で残ったのが $ ❸ = 72 ページ $ということになります。
この72ページが1日目の4目盛り分に当たるので、$ ④ = 72 ページ $となり、$ ① = 18 ページ $となります。
1日目は全体を5としていますので、この本のページ数は $ ⑤ = 90 ページ$となります。
割合を組み合わせる問題
最後に<基礎問題1>~<基礎問題3>を組み合わせた問題について扱います。
ある本を1日目に全体の$ \frac{1}{3} $だけ読み、2日目に28ページだけ読みました。3日目に残りの$ \frac{5}{8}だけ読んだところ、読み残したページが24ページありました。この本は全体で何ページありますか?
まず1日目に対して図を描いてみましょう。
ここは、<基礎問題1>と同じような考え方になります。
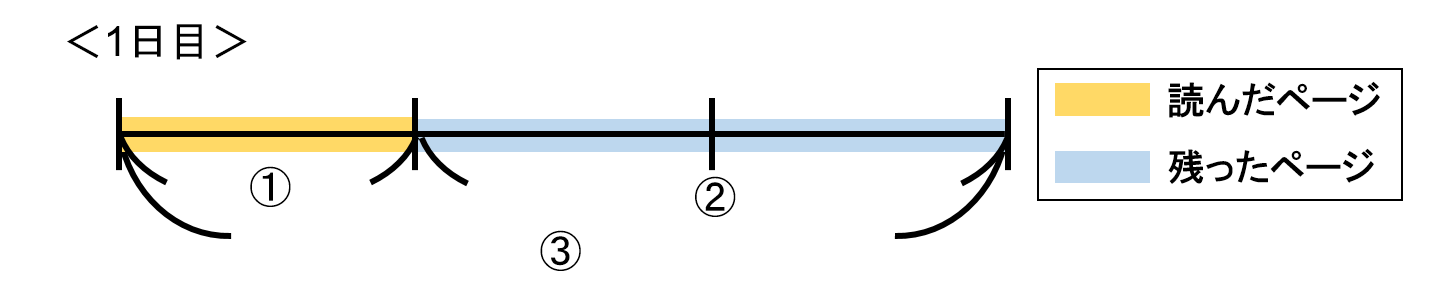
1日目は全体の$ \frac{1}{3} $を読んだので、全体を3としたときの1目盛り分を読んだことになります。
そして。残ったのが2目盛り分になります。
この残ったものを全体として考えると後は<基礎問題2>と同じ考えて方になります。
2日目は割合ではなく読んだページ数が書かれているので、次の図の様になります。
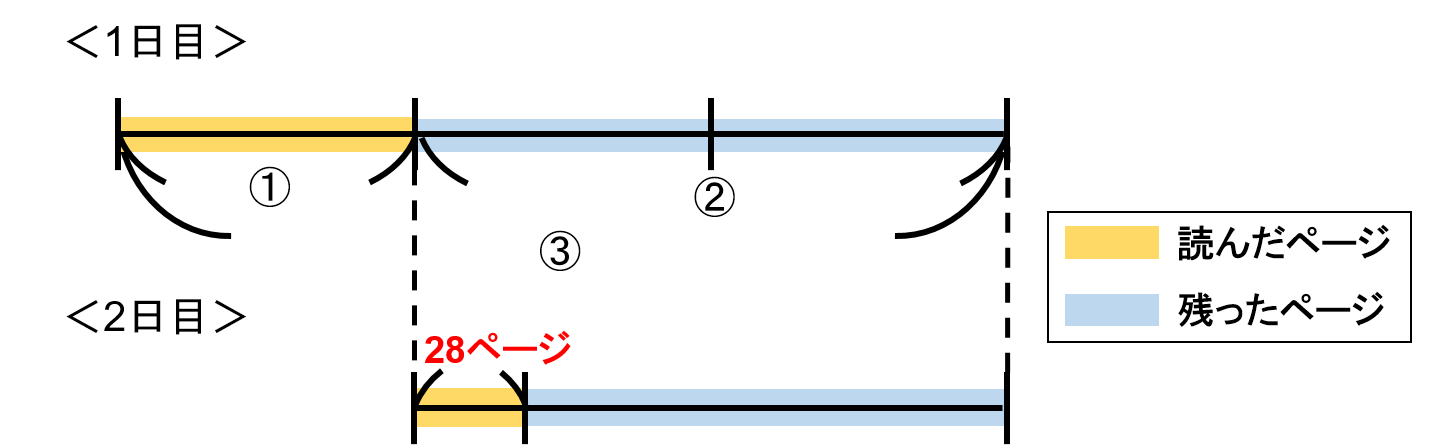
そして、2日読んで残ったページ数に対して$ \frac{5}{8} $を読むので次のようになります。
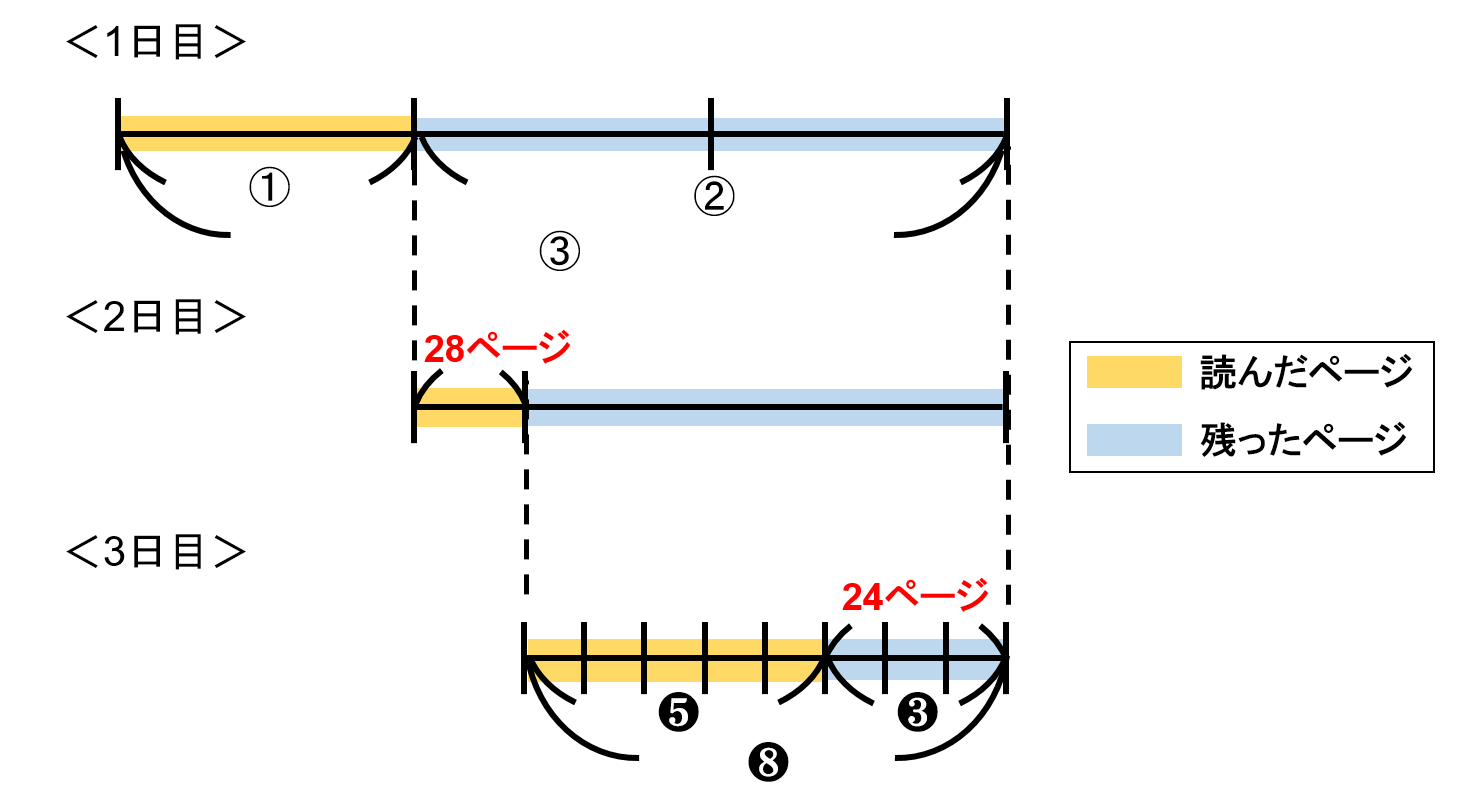
3日目は、2日読んで残ったページ数を8とした時の5目盛り分を読んだので残ったのは3目盛り分になります。
この3目盛りに当たるのが24 ページなので、$ ❸ = 24ページ $となり$ ❶ = 8 ページ $になります。
よって、2日目を読んで残ったページは $ ❽ = 64 ページ $ となるので、1日目で残ったページは $ 64 +28 = 92 ページ $ となります。
この92 ページが1日目に読んで残ったに目盛り分に当たるので、$ ② = 92 ページ $となり $ ① = 46 ページ $となります。
よって、元々あったページ数は$ ③ = 138 ページ $ということになります。
「相当算」の問題を解くうえでは、割合は、何に対してかを考える ことが大切です。
何を基準にして考える必要があるのかを理解するようにしましょう。
次回は、残った割合から全体を求める問題を考えていきたいと思います。








