濃度の異なる食塩水を混ぜたときの濃度を求める問題を考えてみましょう!
濃度の異なる食塩水を混ぜる問題
中学受験を乗り越えるうえで避けられないのが算数です。
算数を苦手とする小学生は多いです。
そんな親御さんも含め小学生でも理解できるように、問題の解き方を基本から解説しています。
前回までに、食塩水の問題を解くうえでの基礎的な考え方について書きました。
濃度って何?
食塩・水・食塩水の重さの出し方
水の蒸発・追加による濃度変化
食塩を加えた時の濃度変化
食塩水の問題は中学受験でよく出題されます。
今回からは、中学入試で出る標準的な問題の考え方・解き方について書いていこうと思います。
「濃度の違う食塩水を混ぜる」問題について、今回は書いていきたいと思います。
<基本問題1>
4%の食塩水300 gと9%の食塩水200 gを混ぜると何%の食塩水になりますか。
<基本問題2>
食塩水が120 gあります。これに10%の食塩水を60 g混ぜたところ、7%の食塩水になりました。はじめの食塩水は何%ですか。
今回は、この2つの問題を考えてみましょう。
では、<基本問題1>から考えていきましょう。
濃度がわかっている食塩水を混ぜる問題
4%の食塩水300 gと9%の食塩水200 gを混ぜると何%の食塩水になりますか。
この問題の考え方の流れは以下になります。
1: 濃度を求めるために、食塩と食塩水全体の重さが必要
2: それぞれの食塩水の重さはわかるが、食塩の重さがわからない
3: それぞれの食塩水に含まれている食塩の重さが必要
問題を解くときは、この考え方の逆になります。
ですので、次のように解いていきます。
1: それぞれの食塩水に含まれている食塩の重さを求める。
2: 最終的な食塩と食塩水全体の重さを求める。
3: 濃度を求める。
では、この順に解いてみましょう。
それぞれの食塩水に含まれている食塩の重さを求める。
<4%の食塩水300 g>

全体が400 gなので、100 = 400gとなり、1 = 4 gということになります。
初めの食塩水の濃度は4 %ですので、4 = 12 gとなり、食塩は12 g含まれていたことになります。
<9%の食塩水200 g>

全体が200 gなので、100 = 200gとなり、1 = 2 gということになります。
初めの食塩水の濃度は9 %ですので、9 = 18 gとなり、食塩は18 g含まれていたことになります。
最終的な食塩と食塩水全体の重さを出す。
「4%の食塩水300 g」には食塩が12 g、「9%の食塩水200 g」には食塩が18 g含まれていることがわかりました。
よって、最終的に食塩は 12 g + 18 g = 30 gであり、食塩水は 300 g + 200 g = 500 gということになります。
濃度を求める。
ここまでの事をまとめると下の図の様になります。
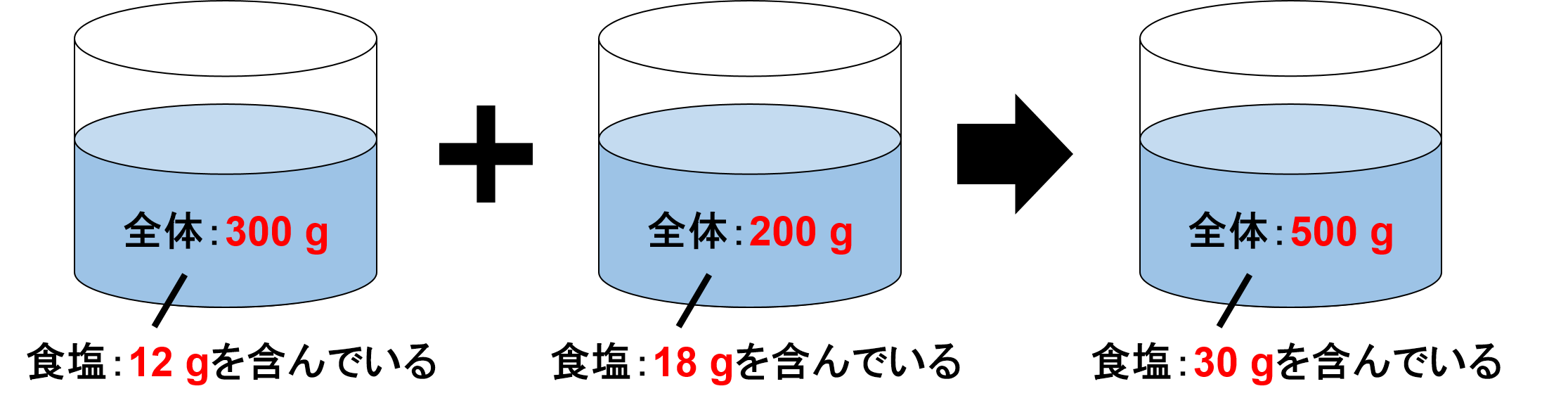
この図から、<基本問題1>は次のような問題だったことがわかります。
食塩を30 g含む食塩水500 gは、何%の食塩水ですか。
ここまで来ると、後は<基礎問題1>と同じ考え方になります。
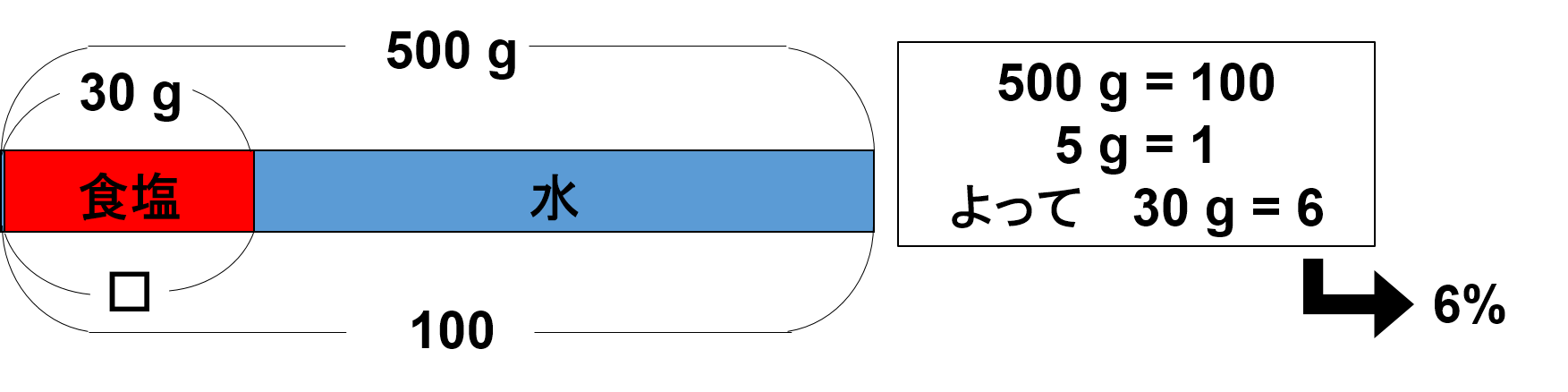
全体が500 gなので500 g = 100となり、5 g = 1となります。
食塩の量が30 gなので、30 ÷ 5 = 6 なので、食塩水の濃度は6%ということになります。
では、続いて<基本問題2>について考えてみましょう。
濃度がわかっていない食塩水を混ぜる問題
食塩水が120 gあります。これに10%の食塩水を60 g混ぜたところ、7%の食塩水になりました。はじめの食塩水は何%ですか。
この問題はまず図にしてみましょう。

<基本問題2>は、混合する前の食塩水の濃度がわかっていないところが<基本問題1>との違いです。
では、この問題はどう解いていくかを考えてみましょう。
この問題の考え方の流れは以下になります。
1: 濃度を求めるために、食塩と食塩水全体の重さが必要
2: 加える前の食塩水は、全体の重さはわかっているが食塩の重さがわからない
3: 加える前の食塩の重さを出すためには、混合後の食塩と加える食塩の重さが必要
4: 濃度と食塩水全体の重さがわかっていれば食塩の量は出せる。
5: 混合後と加える食塩水に含まれる食塩の重さを求める。
問題を解くときは、この考え方の逆になります。
ですので、次のように解いていきます。
1: 混合後と加える食塩水に含まれている食塩の重さを求める。
2: 加える前の食塩水の全体と食塩の重さを求める。
3: 濃度を求める。
では、この順に解いてみましょう。
混合後と加える食塩水に含まれる食塩の重さを求める。
混合後と加える食塩水に含まれる食塩の重さは、濃度と全体の重さから求めることが出来ます。
<混合後の食塩水>
混合後の食塩水は、濃度が7%です。食塩水全体の重さは、120 gの食塩水に60 gの食塩水を加えているので120 g + 60 g = 180 gということになります。
よって、次の図のようになります。

全体が180 gなので、1 = 1.8 gになります。
今回は濃度が7 %なので、1.8 g × 7 = 12.6 g の食塩が含まれていることになります。
<加える食塩水>
加える食塩水は、濃度が10%で食塩水全体の重さは60 gです。

全体の重さが60 gなので、100 = 60 gから1 = 0.6 gとなります。
今回は濃度が10 %なので、10 = 6 gとなり、含まれている食塩の重さは6 gとなります。
加える前の食塩水の全体と食塩の重さを求める。
混合後と加える食塩水に含まれる食塩の重さを求めることができました。
ここまでを一旦図にしてみましょう。
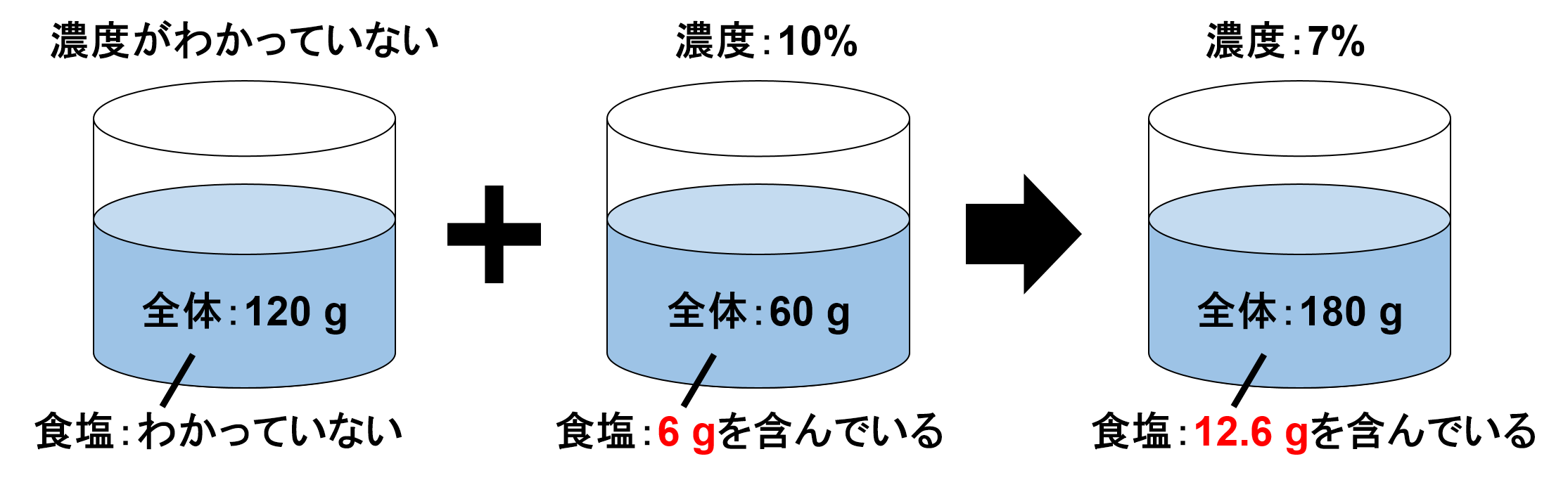
図を見てみると、混合後の食塩の重さが12.6 gで、加える食塩の量が6 gということがわかります。
6 gの食塩を加えて、12.6 gになっているので、加える前の食塩の重さは、12.6 g – 6 g = 6.6 gということになります。
濃度を求める。
ここまでの事をまとめると下の図の様になります。
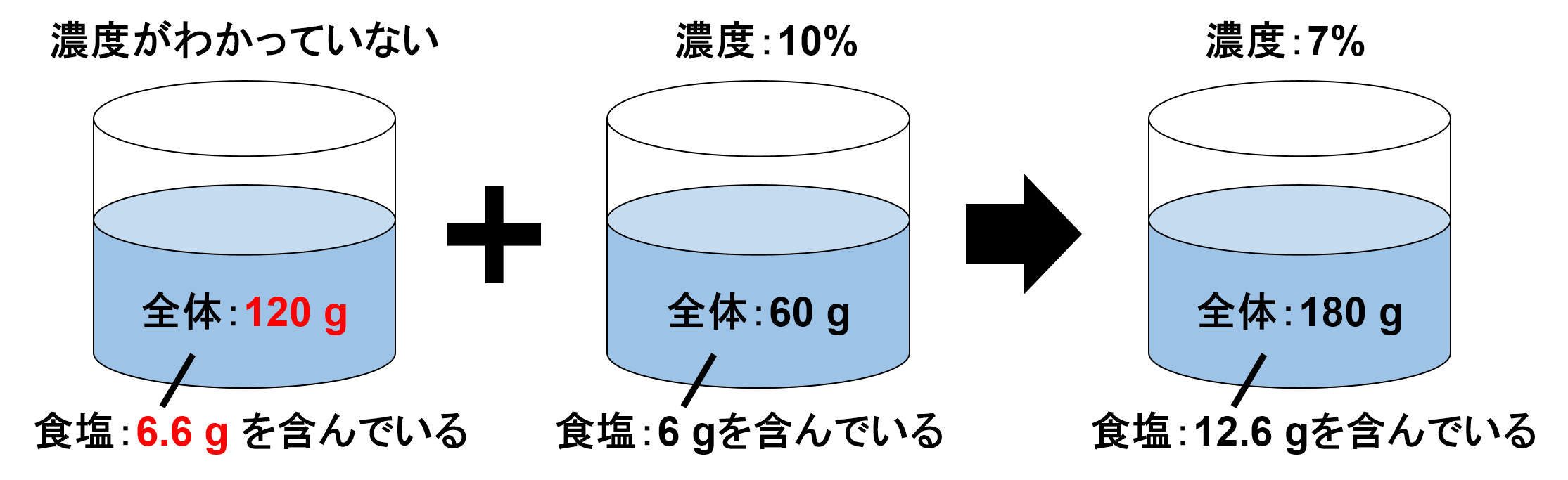
ここまで来ると、<基本問題2>は次のような問題と同じです。
食塩を6.6 g含む食塩水120 gは、何%の食塩水ですか。
ここまで来ると、後は<基礎問題1>と同じ考え方になります。
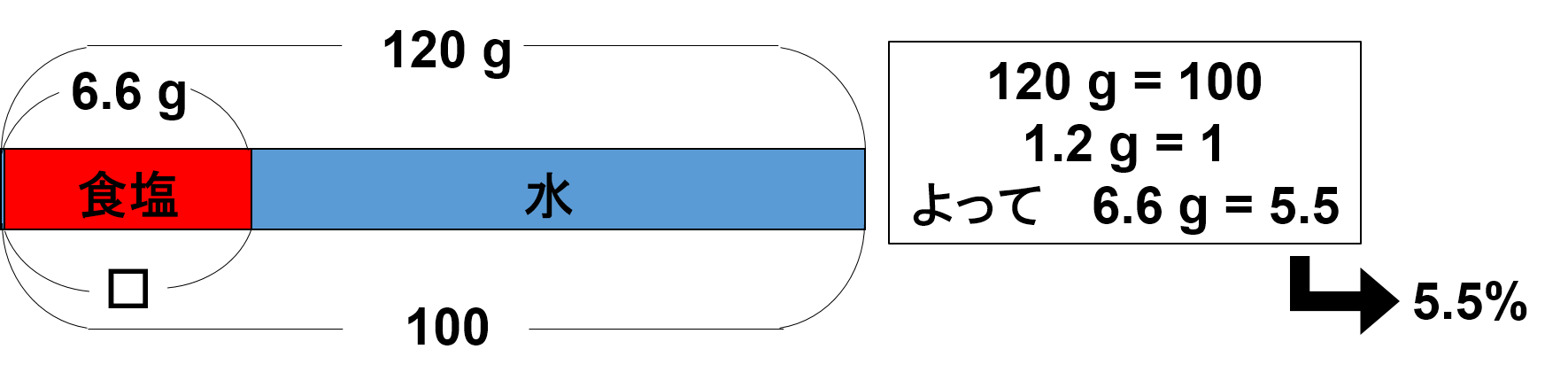
全体が120 gですので、120 g = 100となり、1.2 g = 1となります。よって、6.6 g ÷ 1.2 g = 5.5となるので、加える前の食塩水の濃度は5.5% となります。
今回は「濃度の違う食塩水を混ぜる」問題について考えました。
この問題を解くうえで大事なことは、 食塩の量 に注目することです。
<基礎問題1> ~ <基礎問題7>の考え方を用いて、それぞれの食塩の重さを算出することが今回の問題のポイントです。
食塩の重さと食塩水全体の重さを求めれば濃度を出すことができるとうことをしっかり意識しましょう。
次回は、「加えた食塩水の濃度を求める問題」について考えていこうと思います。
食塩水問題の基礎的な考え方はこちら↓







