『旅人算』の基本的な考え方 その2
中学受験を乗り越えるうえで避けられないのが算数です。
算数を苦手とする小学生は多いです。
そんな親御さんも含め小学生でも理解できるように、問題の解き方を基本から解説しています。
前回は、「同じ方向に進む」「逆方向に進む」ときの考え方について書きました。
向かい合って歩いた時出会うのにかかる時間は?
<基本問題3>
兄は家から駅まで分速100 m、弟は駅から家まで分速80 mの速さで、歩きます。家から駅までの距離が3240 mのとき、同時に出発した2人が出会うのは何分後ですか。
今回は、この問題を考えてみましょう。
<考え方1> 2人が出会うとはどうゆうこと?
そもそも出会うというのはどういうことでしょうか。
次の図を見てください。

初め2人は1000 m離れています。そこからお互い歩き始めます。
では2人が少し歩くとどうなるでしょうか?
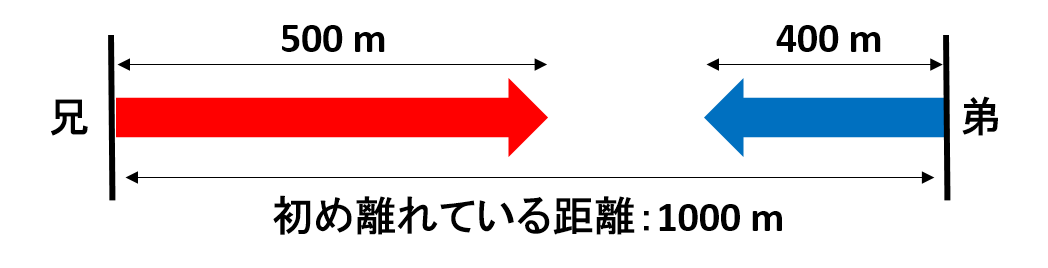
兄が500 m歩き、弟が400 m進んだとします。
そして2人の距離は、進んだ分近づくので1000 m – 500 m – 400 m = 100 m離れていることになります。
では出会った時はどうなるでしょうか?
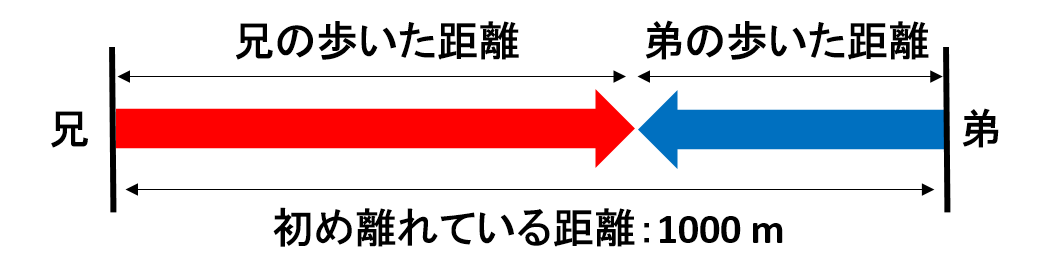
出会ったとき、2人の離れている距離が0 mになります。
ここで、兄が歩いた距離は赤色のの矢印、弟が歩いた距離が青色の矢印になります。
この図から、2人が歩いた距離の合計が初めに離れていた距離になれば出会うことができるということがわかります。
- 出会う:「二人が歩いた距離の合計」=「初めに離れた距離」
<考え方2> 2人が1分で歩く合計は?
分速とは、1分間で進む距離の事です。
今回は、兄は1分間で100 m進み、弟は1分間で80 m進みます。
では、1分後に2人はどれだけ歩くでしょうか?
<1分後>

図から、1分後には兄と弟で、100 m + 80 m = 180 m 歩くことがわかります。
つまり、今回2人は合わせて1分間で180 m歩くことになります。
<考え方3>2人が出会うまでの時間は?
ここまでで、「出会うということは、2人が歩く距離の合計が初め離れていた距離になること」「2人は1分で合計180 m歩く」ということがわかりました。
そして、2人が初め離れていた距離は3240 mでした。
つまり、今回の問題は以下のような問題と同じです。
<基礎問題3> 兄と弟は1分間で合計180 m歩きます。3240 m歩くのにかかる時間は何分ですか?
<解き方>
出会うまでにかかる時間を□分とします。
1分で180 m進むので□分で、180 × □ m歩くことになります。
これが3240 mになるので、
180 × □ = 3240 m ⇔ □ = 3240 ÷ 180 = 18
よって、答えは 18 分 ということになります。
ここまでが、旅人算を解くための基本になります。
<基礎問題1> ~ <基礎問題3>をしっかり理解しておくことで、応用問題も解ける様になります。
では、試しによく出る池の周りを歩く問題を解いてみましょう。
池の周りを反対向きに歩いて出会うまでの時間は?
続いて、次の問題について考えてみましょう。
<標準問題1>
1周2400 mの池の周りをAさんは分速70 m、B君は分速 50 mで同じ場所から同時に反対方向に進みました。2人が出会うのは何分後ですか。
<考え方1>出会うってどうゆうこと??
先ほど出会うという事を考えたように、出会うとはどうゆうことか考えてみましょう。
今回はいきなり出会った時ときの図を書いてみましょう。
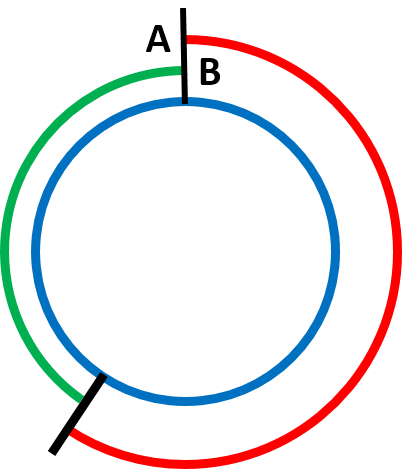
円では分かりにくいのでスタート地点で切って直線にしてみましょう。

このように直線に書き換えてみれば、先ほど考えた<基礎問題3>と同じような図になりました。
つまり、池の周りを反対方向に歩いて出会うというのは2人の進んだ距離の和を考えれば良いということがわかります。
では、出会った時2人の進む距離の差はどれだけになるでしょうか?
もう一度円を見てください。

すると2人の距離の差は、円1周分と同じことがわかります。
このことから、「池の周りを反対方向に歩いて出会う」ということは「2人の進んだ距離の和が池の1周分の長さになる」事だということがわかります。

- 出会う:「2人の進んだ距離の和」=「池の1周分の長さ」
<考え方2> 2人が1分で歩く合計距離は?
先ほどと同じように、2人が1分で歩く合計距離を考えます。
分速とは1分で進む距離のことですので、Aさんは1分で70 m、Bさんは1分で50 m進みます。
ですので、AさんとBさんの歩く距離の和は1分で120 mということになります。

追いつくまでの時間は??
先ほどのことから、池の周りを反対方向に歩いて出会う」ということは「2人の進んだ距離の和が池の1周分の長さになる」ということがわかりました。
そして、「2人が1分で進む距離の和は120 m」ということがわかり、今回の池1周分の距離は2400 mです。
このことから、<標準問題1>の問題は以下の問題と同じということになります。
<標準問題1>
AさんとBさんは1分間で2人で合計120 m 歩きます。2人の歩く距離距離の和が2400 mになるのにかかる時間は何分ですか?
では解いてみましょう。
<解き方>
出会うまでにかかる時間を□分とします。
1分で120 m 歩くので、□分で120 × □ m 進むことになります。
これが2400 mになるので、
120 × □ = 2400 m ⇔ □ = 2400 ÷ 120 = 20
よって、答えは 20 分 ということになります。
池の周りを回る問題は、一見新しい問題の様に感じます。
しかし、直線に変えてしまえば<基礎問題3>と同じ考え方で解けるということがわかります。
2回にわたって旅人算の基本的な考え方について書きました。
まずは、<基礎問題1> ~ <基礎問題3>をしっかり理解できるようにしてください。
公式を当てはめて解くのではなく、「どうして同じ方向に進むときは速度の差を求めるのか」「どうして反対方向で進むときは速度の和を求めるのか」を理解しながら解けるようにしてください。
一見難しい問題に感じても、結局やることは<基礎問題1> ~ <基礎問題4>と同じです。
次回旅人算の標準~応用問題についても書いていきたいと思いますが、まずはしっかり<基礎問題1> ~ <基礎問題3>を理解するようにしてください。




