『旅人算』の基本的な考え方

中学受験を乗り越えるうえで避けられないのが算数です。
大学受験や高校受験に比べて中学受験は親御さんの支えがとても重要になります。

しかし、子どもがわからないと言っているけど教え方がわからなかったりするともどかしい思いをしませんか。

そんな親御さんも含め小学生でも理解できるように、問題の解き方を基本から解説しています。

少しでも中学受験を家族で乗り切ろうとしている人の役に立てればと思っています。

今回は小学生が理解できにくい「旅人算」について書いてみたいと思います。

私は子ども達に教える際に、テクニックや解き方を教えることを最優先にしていません。
まずは、どうしてそうなるのかを考えてもらうようにしています。

ですので、この記事には「○○秒で解けるようになる」といったような解き方は説明していません。

テクニックを覚えただけでは、問題が変わると解けないということが起こりやすいです。

ですので、基本から理解して欲しいと思っています。

Contents

同じ方向に歩いて離れるのにかかる時間は？

まずは、この問題を考えてみましょう。

分速とは、1分間で進む距離の事です。
つまり、兄は1分間で96 m進み、弟は1分間で72 m進みます。

では、1分後に2人はどれだけ離れるでしょうか？
＜1分後＞

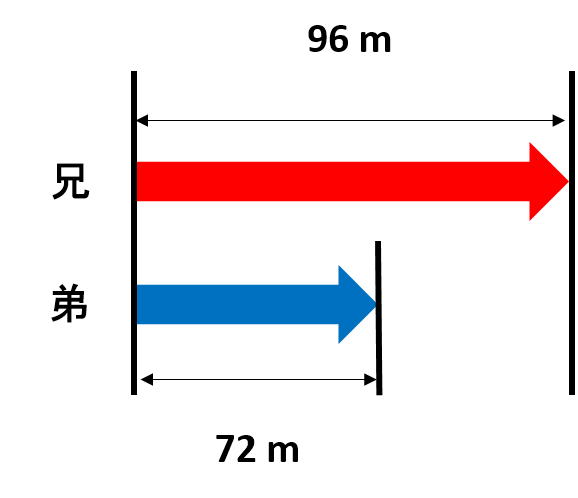
図から、1分後には兄と弟で、96 m-72 m = 24 m 離れることがわかります。

先ほどと同じように2分後を図で考えてみましょう。

＜2分後＞

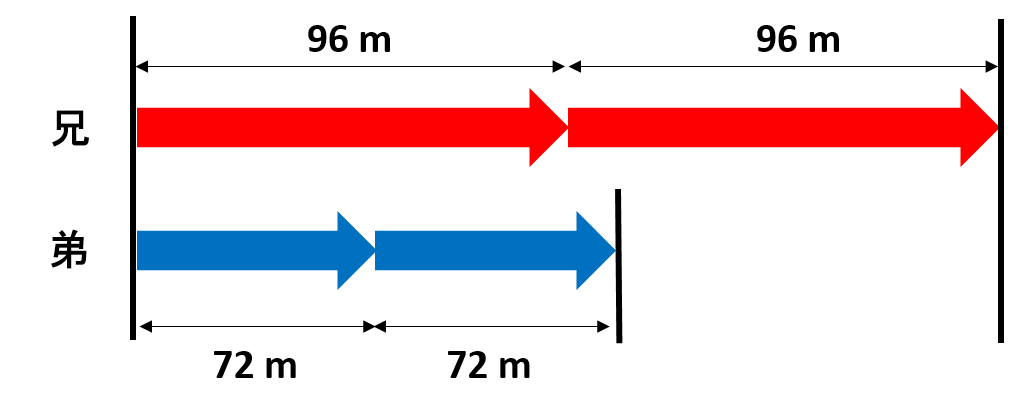
図のように、兄は 96 m × 2分 = 192 m 進み、弟は、72 m × 2 分 = 144 m進みます。
ですので、2人は、192 m – 144 m = 48 m離れることになります。

では20分後はどうなるでしょうか。

＜20分後＞

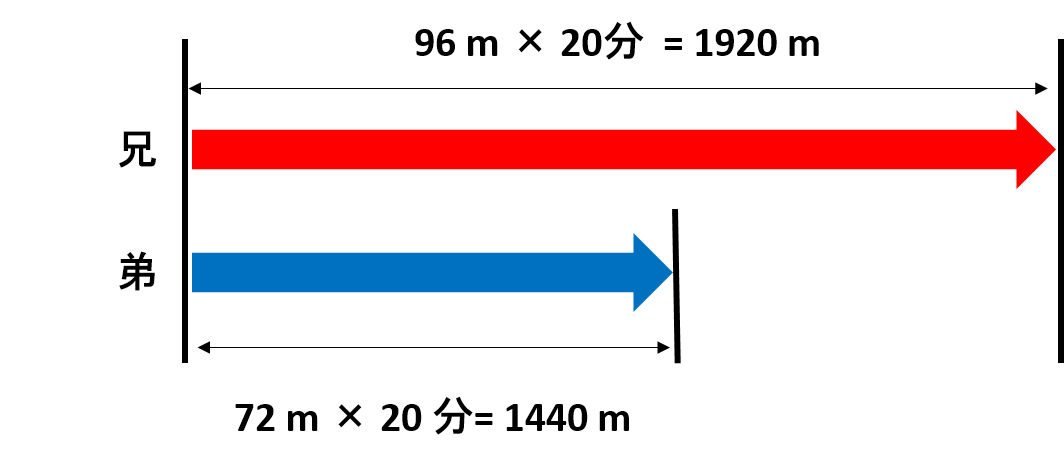
兄は1920 m、弟は1440 m進むので、1920 m – 1440 m = 480 m離れることになります。

ここまでで、1分で24 m、2分で48 m、20分で 480 m 離れることがわかりました。
このことからわかることは、24にそれぞれの時間を掛けた値になっています。
では、この24という数字はどこから出てくるのか、それは2人の速度差です。

先ほども書きましたが、分速とは1分で進む距離です。
ですので、速度の差は1分で2人が離れる距離になります。
このことから、今回は96 – 72 = 24 m （2人の速度差）だけ1分で離れることになります。

では、今回の問題にある2856 m 離れるのにかかる時間はどれくらいでしょうか？

＜考え方3＞から、1分間で24 m離れることがわかりました。
では、求める時間を□分だとすると

　24 × □ = 2856 ⇔　□ = 2856 ÷ 24 ⇔ □ = 119

よって、119分後ということになります。