基本的な考え方 その2
中学受験を乗り越えるうえで避けられないのが算数です。
算数を苦手とする小学生は多いです。
そんな親御さんも含め小学生でも理解できるように、問題の解き方を基本から解説しています。
今まで複数回に分けて、「旅人算」「食塩水の問題」「仕事算」「過不足算」「相当算」の基本的な考え方について書いてきました。
今回は、「過不足算」でよくある長椅子の問題の解き方について書いていきたいと思います。
過不足から生徒の人数を求める
今回は長椅子に3人がけした場合と5人掛けした場合の過不足から生徒の人数を求める問題を考えていきましょう。
<基礎問題6>
長椅子が10脚あります。1脚に5人掛けしたときと3人掛けしたときで座れる人数は何人変わりますか。
<基礎問題7>
長椅子が何脚かあります。この長椅子に生徒を全員座らせようと思います。1脚に7人掛けするとちょうど座れ、5人掛けにすると20人座れませんでした。長椅子は何脚ありますか。
<基礎問題8>
長椅子が何脚かあります。この長椅子に生徒を全員座らせようと思います。1脚に7人掛けするとあと30人座れ、5人掛けするとちょうど座れました。長椅子は何脚ありますか。
<基礎問題9>
長椅子が何脚かあります。この長椅子に生徒を全員座らせようと思います。1脚に5人掛けすると、ちょうど15人座れず、7人掛けすると、35人分の座席が余りました。長椅子は何脚ありますか。
基本的な考え方は、<基礎問題1>~<基礎問題5>と同じになります。
次回以降長椅子を用いた基本問題等を解くうえで必要な考え方になりますのでしっかり理解してください。
それでは、<基礎問題6>から考えていきましょう。
1脚に座る人数を変えるとどうなるか
<基礎問題6>は<基礎問題1>と同じような問題です。
この問題を通してもう一度、配る量を変えることでどれだけの差が生まれるかについて見ていきましょう。
この考え方が過不足算を解くうえでの1番の基本になります。
<基礎問題6>
長椅子が10脚あります。1脚に5人掛けしたときと3人掛けしたときで座れる人数は何人変わりますか。
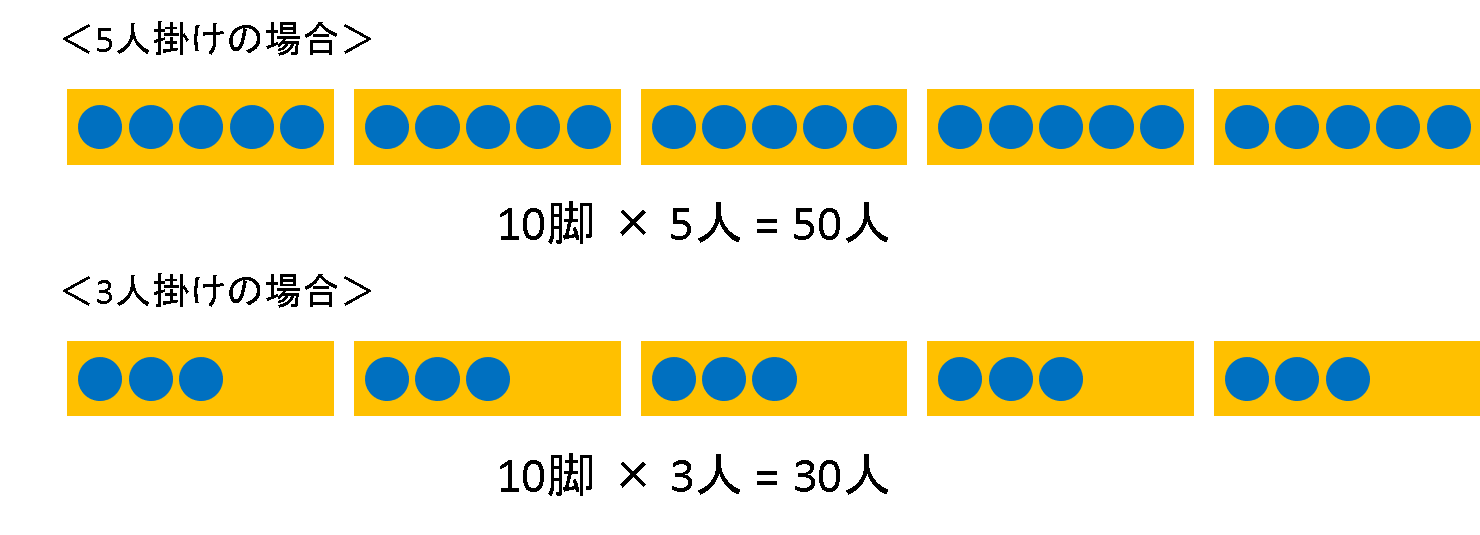
10脚に5人ずつ座ると10脚times5人=50人、3人ずつ座ると 10脚times3人=30人座ることができます。
つまり、50人–30人=20人になります。
答えを出すだけであれば簡単な掛け算と引算で出すことができます。
ここで下の図を見て下さい。
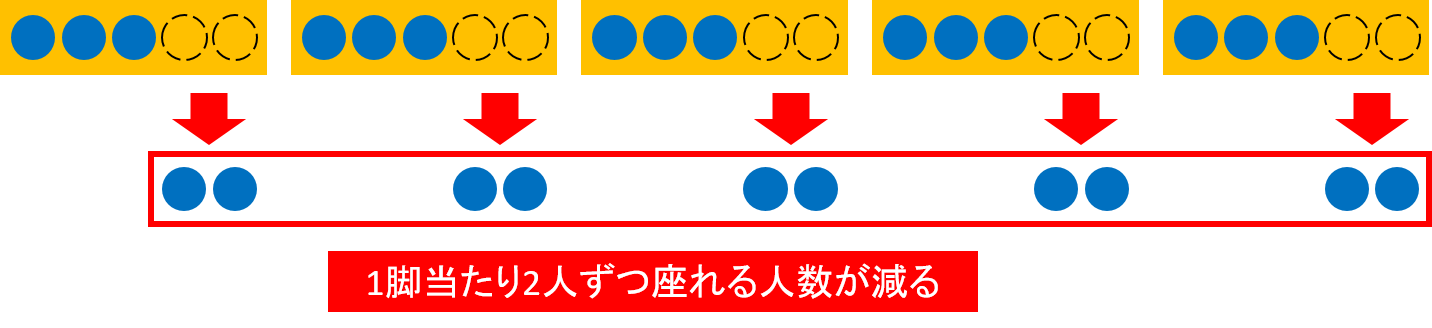
この図のように、5人から3人にすることで1脚2人ずつ座れる人数が減ると考えることが重要になります。
1脚2人ずつ減るので、10脚times2人=20人減るという考え方が過不足算の基本になります。
このように過不足算では、1つ当たりの数が変化すれば、変化した数×個数分必要な数が変化するということが大切な考えになります。
長椅子の問題では、1脚当たりの座る人数が変化すると、「その変化した人数 × 長椅子の数」だけ座れる人数が変化します。
では、この考えを基に<基礎問題7>を解いてみましょう。
座れなかった人数から長椅子の数を求める
<基礎問題7>は座れなかった人数から長椅子を求めていきます。
<基礎問題7>
長椅子が何脚かあります。この長椅子に生徒を全員座らせようと思います。1脚に7人掛けするとちょうど座れ、5人掛けにすると20人座れませんでした。長椅子は何脚ありますか。
考え方
7人掛けするとちょうど全員が座ることができました。
一方、5人掛けすると20人が座れませんでした。
つまり、7人掛けした時と3人掛けした時とで座ることが出来る人数が20人減ったということになります。
ここで、7人掛けと5人掛けでは1脚当たりの人数は2人減少することになります。
よって、長椅子の数を□脚とすると2人times□脚減少するということになります。
今回は20人減ったとあるので、2times□=20となります。
このことから、子どもの人数は□=20div2=10脚 ということになります。
図を用いて解いてみる
<基礎問題7>を長方形の面積を用いて解くことができます。
次の図を見てください。

赤枠の面積が生徒の数を表しています。
縦に長椅子の数である□脚、横に1脚に座った人数を取ります。
長方形の面積は、縦times横で表せるので、横に7人をとった時の面積7times□が、7人掛けする際に座ることができる人数になります。
今回は7人掛けではちょうど全員座ることができたので、7人掛けした時の面積と生徒の数が同じになっています。
そして、5人掛けの時に座ることができる人数が薄い青色の面積5人times□になります。
この図から、赤枠と青色の面積の差である黄色の部分が座れなかった人数になります。
黄色の部分の横の長さは、7人–5人=2人にあたります。
この横の長さは、7人から5人にしたときの1脚当たりの変化量になります。
黄色の面積は2times□で表すことができ、今回は20人座れなくなったので2times□=20となります。
よって、長椅子の数は□=20div2=15脚 ということになります。
過不足算は面積図を用いて解くことができますが、どうして図の様になるのかを理解してから解くようにしてください。
続いて、余った座席数から長椅子の数を求めてみましょう。
余った座席数から長椅子の数を求める
<基礎問題7>では、座れなくなった人数から長椅子の数を求めました。
<基礎問題8>では、余った座席数から長椅子の数を求めます。
<基礎問題8>
長椅子が何脚かあります。この長椅子に生徒を全員座らせようと思います。1脚に7人掛けするとあと30人座れ、5人掛けするとちょうど座れました。長椅子は何脚ありますか。
考え方
5人掛けするとちょうど全員座ることができましたが、7人掛けにすると30人分座席が余りました。
つまり、30人分座ることができる座席数が増えたということになります。
また、5人掛けから7人掛けにすることで1脚当たりに座ることが出来る人数が2人ずつ増えます。
よって、長椅子の買うを□脚とすると2人times□脚=30ということになり、□=30div2=15脚ということになります。
図を用いて解いてみる
<基礎問題8>も<基礎問題7>と同様に長方形の面積を用いて解くことができます。
次の図を見てください。
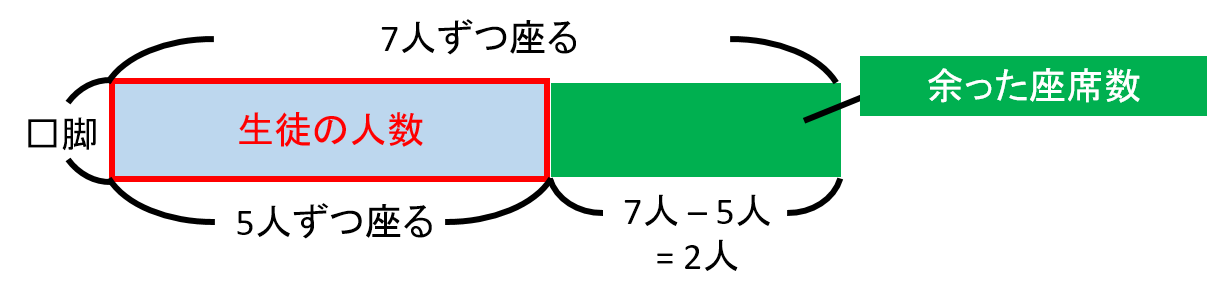
赤枠の面積が生徒の人数とします。
そして、縦に長椅子の数である□脚、横に1脚に座った人数を取ります。
今回は5人掛けした時にちょうど座ることができたので、5人掛けした時の面積と生徒の人数が同じになっています。
そして、7人掛けした時に座ることができる人数にあたるのが、青色と緑色の部分の面積の和7times□になります。
そうすると、緑色の部分が余った座席数になります。
緑色の部分の横の長さは、7人–5人=2人にあたるので、面積は2times□で表すことができます。
今回は、30人分の座席が余ったので2times□=30となり、求める長椅子の数は□=30div2=15脚 ということになります。
<基本問題7>と<基本問題8>は、座れない人数もしくは余った座席数のどちらかのみから長椅子の数を求めました。
次は、片方では座れない生徒がいて、もう片方では座席が余る問題について考えてみましょう。
座れない生徒と余った座席数から長椅子の数を求める
<基礎問題9>では、座れない生徒数と余った座席数から長椅子の数を求めます。
<基礎問題9>
長椅子が何脚かあります。この長椅子に生徒を全員座らせようと思います。1脚に5人掛けすると、ちょうど15人座れず、7人掛けすると、35人分の座席が余りました。長椅子は何脚ありますか。
考え方
この問題では、5人掛けと7人掛けで座ることのできる人数はどう変化しているでしょうか。
5人掛けでは15人が座れず、7人掛けでは座席が35人分余ります。
つまり、5人掛けと7人掛けで15+35=50人 座ることが出来る人数が増えているということになります。
5人掛けと7人掛けで1脚当たり2人ずつ座ることができる人数は増えます
ですので、長椅子の数を□脚とすると、2times□=50となり、□=50div2=25脚ということになります。
図を用いて解いてみる。
<基礎問題9>も長方形の面積を用いて解くことができます。
次の図を見てください。
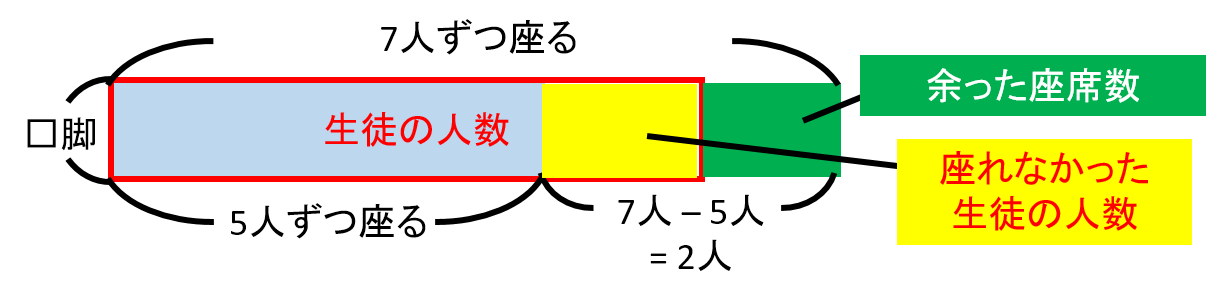
今までと同じように赤枠の面積が生徒の人数になります。
そして、縦に長椅子の数である□脚、横に1脚あたりの人数を取ります。
横に5人をとった時(青色の部分)の面積5times□が、5人掛けで座ることができる人数になります。
そして、5人ずつ座った時に座ることができる人数にあたるのが赤色の枠と緑色を足した面積7times□になります。
そうすると、緑色の部分が余った座席数であり、黄色の部分が座れなかった生徒の人数になります。
黄色と緑色の部分の横の長さは、7人–5人=2人にあたるので、面積は2times□で表すことができます。
今回は5人掛けで座れなかった人数が15人、7人掛けで余った座席数が35人分なので、2times□=15+35=50となり、求める子どもの人数は□=50div2=25脚 ということになります。
今回は「過不足算」でよく見る長椅子の問題について書きました。
<基礎問題1>~<基礎問題5>と基本的には同じ考え方です。
次回は長椅子を使った標準問題を扱います。
その際に、<基礎問題6>~<基礎問題9>の考え方が必要になりますのでしっかり理解しておいてください。
過不足算の過去記事はこちら↓









