[usemath]
『仕事算』の基本的な考え方 その1
中学受験を乗り越えるうえで避けられないのが算数です。
算数を苦手とする小学生は多いです。
そんな親御さんも含め小学生でも理解できるように、問題の解き方を基本から解説しています。
今まで複数回に分けて、「旅人算」「食塩水の問題」について書いてきました。
旅人算:同じ向きと逆向きに歩く違い
食塩水:濃度とは?百分率とは?
今回は、「仕事算」の基本的な考え方について書いていきたいと思います。
1日の仕事量とかかる時間を求める。
仕事算を解くうえで必要になる「1日の仕事量」と「終わらせるのにかかる時間」について考えていきましょう。
<基本問題1>
ある仕事を仕上げるのに、Aさんだけでは5日かかります。全体の仕事量を1とするとAさんは1日でどれだけの仕事量を終わらせることができますか。
<基礎問題2>
ある仕事を仕上げるのに、Aさんだけでは5日かかり、Bさんだけでは10日かかります。全体の仕事量を1とするとAさんBさんが一緒に仕事をすると1日でどれだけの仕事量を終わらせることができますか。
<基本問題3>
ある仕事を仕上げるのに、Aさんだけでは20日かかり、Bさんだけでは30日かかります。この仕事をA, B2人ですると何日で終わりますか。
<基本問題4>
ある仕事を仕上げるのに、Aさんだけでは20日かかり、Bさんだけでは30日かかります。この仕事をAさんが$\frac{1}{3}$終わらせました。残りの仕事をBさんが終わらせるのに何日かかりますか。
では、<基礎問題1>から解いていきましょう。
1日の仕事量を求める。
仕事算を考えるうえで必ず必要になるのが「1日の仕事量」です。
そして、次のことが仕事算を解く上で大切になります。
- 全体の仕事量を1として考える
最小公倍数を用いて仕事量を整数で求める方法もありますが、私は全体の仕事量を1として考えることをオススメしています。
では、この考え方をもとに<基礎問題1>を解いてみましょう。
<基本問題1>
ある仕事を仕上げるのに、Aさんだけでは5日かかります。全体の仕事量を1とするとAさんは1日でどれだけの仕事量を終わらせることができますか。
下の図を見てください。

Aさんは、5日間かけてすべての仕事を終わらせることができます。
毎日同じ量だけ仕事をするので、1日で終わらすことのできる仕事量は $1\div5=\frac{1}{5}$ということになります。
つまり、Aさんは1日$\frac{1}{5}$ずつ仕事をするので、$\frac{1}{5}+\frac{1}{5}+\frac{1}{5}+\frac{1}{5}+\frac{1}{5}=1$となり全体の仕事量1を終わらせるということになります。
では、続いて<基礎問題2>を考えてみましょう。
複数人で仕事をしたときの1日の仕事量を求める
先ほどは、1人でする仕事量を求めました。
続いて考える問題は複数人で仕事をしたときの1日の仕事量です。
この問題も、全体の仕事量を1として考えます。
<基礎問題2>
ある仕事を仕上げるのに、Aさんだけでは5日かかり、Bさんだけでは10日かかります。全体の仕事量を1とするとAさんBさんが一緒に仕事をすると1日でどれだけの仕事量を終わらせることができますか。
Aさん1人でこの仕事を仕上げようと思うと5日かかります。
ですので、Aさんが1日でできる仕事量は$1\div5=\frac{1}{5}$といいうことになります。
同じように考えるとBさんが1日でする仕事量は$1\div10=\frac{1}{10}$ということになります。
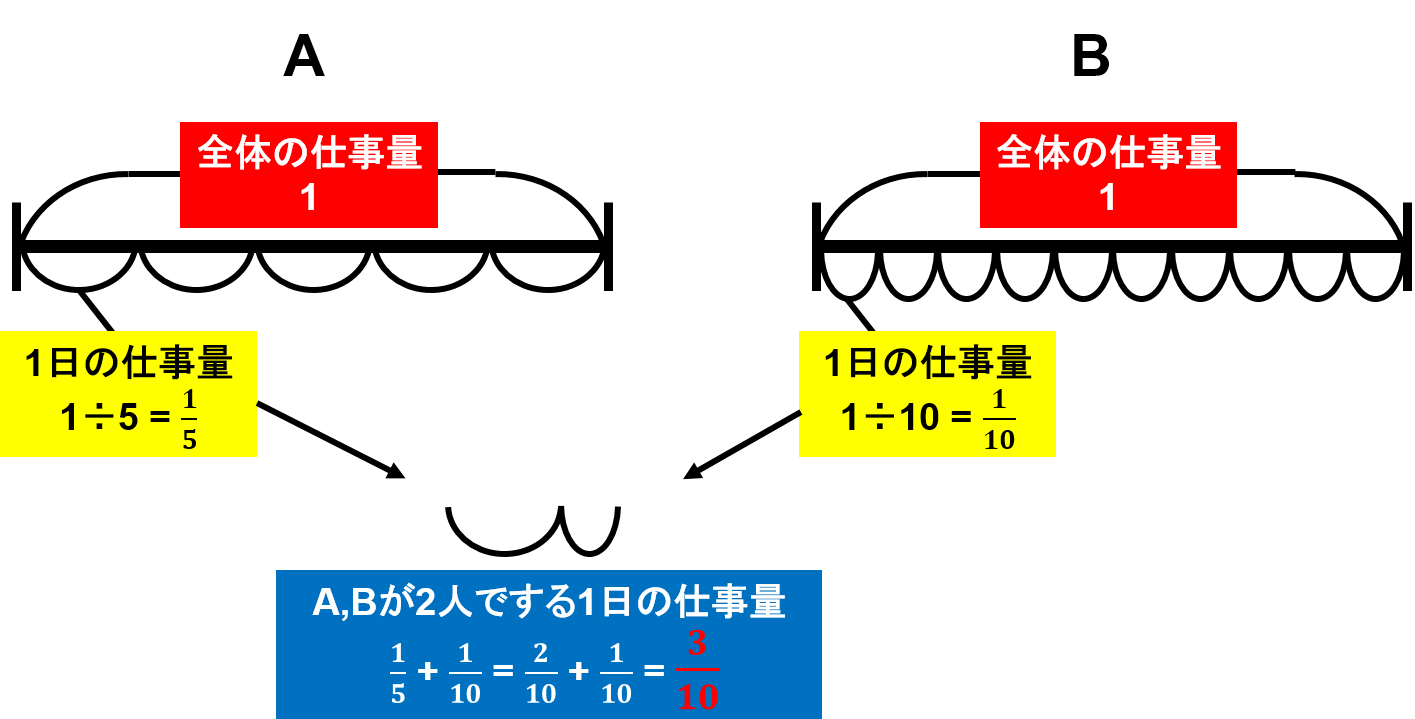
Aさんは1日で$\frac{1}{5}$、Bさんは1日で$\frac{1}{10}$仕事を終わらせることができます。
よって、A, B2人で$\frac{1}{5}+\frac{1}{10}=\frac{2}{10}+\frac{1}{10}=\frac{3}{10}$となります。
では、この考え方を使って<基礎問題3>を考えてみましょう。
全部の仕事を終わらせるのにかかる日数を求める。
ここまでで、1人および複数人で仕事をした場合に1日で終わらすことのできる仕事量について考えました。
次は、その考え方を用いて全部の仕事を終わらせるのにかかる日数について考えます。
<基本問題3>
ある仕事を仕上げるのに、Aさんだけでは20日かかり、Bさんだけでは30日かかります。この仕事をA, B2人ですると何日で終わりますか。
まず、「仕事算」の問題を解くうえで大切な考え方に2つ目が以下になります。
- 仕事をする日数を出すには、1日の仕事量が必要
今回は、A, B2人で終わらせる日数ですので「A, B2人が1日でする仕事量」が必要になります。
では、<基礎問題1><基礎問題2>の考え方を用いて「A, B2人が1日でする仕事量」を出してみましょう。
Aさんは20日でこの仕事を終わらせることが出来ます。
ですので、Aさんが1日でできる仕事量は$1\div20=\frac{1}{20}$といいうことになります。
同じように考えるとBさんが1日でする仕事量は$1\div30=\frac{1}{30}$ということになります。
これから、A, B2人では1日で$\frac{1}{20}+\frac{1}{30}=\frac{3}{60}+\frac{2}{60}=\frac{5}{60}=\frac{1}{12}$終わらせることができることになります。
これで、「A, B2人が1日でする仕事量」を出すことができました。
ではこれを使って仕事を終わらせるのにかかる時間を出してみましょう。
全体の仕事量を1としていますので、A, B2人がする仕事量が1になれば仕事が終わったことになります。
A, B2人で仕事をすると1日で$\frac{1}{12}$仕事をすることができますので、12回繰り返せば1となり仕事を終わらせることが出来ます。
つまり、A, B2人では12日で仕事を終わらせることができるということになります。
全体の仕事を終わらせるためには、1になるように考えればかかる時間を出すことができました。
では、一部の仕事をする場合はどうしたらいいかを<基礎問題4>を使って考えてみましょう。
残りの仕事を終わらせるのにかかる時間を求める。
ある仕事を誰かがやった残りを終わらせるのにかかる時間を求める問題について考えてみましょう。
<基本問題4>
ある仕事を仕上げるのに、Aさんだけでは20日かかり、Bさんだけでは30日かかります。この仕事をAさんが$\frac{1}{3}$終わらせました。残りの仕事をBさんが終わらせるのに何日かかりますか。
ここまで書いた「仕事算」の問題を解くうえで大切な以下の考え方をもとに解いていきましょう。
- 全体の仕事量を1として考える
- 仕事をする日数を出すには、1日の仕事量が必要
今回はBさんが終わらせるのにかかる日数を求めるので、まずBさんが1日でする仕事量について求めます。
Bさんは、全部の仕事を終わらせるのに30日でかかるので、1日でする仕事量は$\frac{1}{30}$になります。
<基礎問題3>との違いは、全部の仕事量をするのではなくAさんが残した仕事をする点です。
ここで「仕事算」の問題を解くうえで大切な考え方の3つ目がこれです。
- 仕事をする日数を出すには、する仕事量が必要
Aさんは全部の仕事の$\frac{1}{3}$を終わらせたので、Bさんがする仕事量は$1-\frac{1}{3}=\frac{2}{3}$になります。
では、$\frac{2}{3}$の仕事量を終わらせる日数はどうやって出せばいいでしょうか。
今回Bさんは、1日で$\frac{1}{30}$の仕事量を終わらせることができ、仕事量が$\frac{2}{3}$になれば仕事が終わることになります。
つまり、$\frac{2}{3}$になるまで$\frac{1}{30}$を加えた回数が仕事を終わらせるまでの日数になります。
言い方を変えると、$\frac{2}{3}$のなかに$\frac{1}{30}$が何個あるかを考えればいいことになります。
ここで、「仕事算」の問題を解くうえで大切な考え方に4つ目がいかになります。
- する仕事量 ÷ 1日の仕事量 = かかる日数
今回は、する仕事が$\frac{2}{3}$、1日の仕事量が$\frac{1}{30}$ですので、かかる日数は次のようになります。
$$\frac{2}{3}\div\frac{1}{30}=\frac{2}{3}\times\frac{30}{1}=20$$
よって、残った仕事をBさんがするのにかかる日数は20日ということになります。
今回は「仕事算」の問題を解くうえで必要な「1日でする仕事量」と「仕事を終わらせるのにかかる時間」について書きました。
仕事算の問題は、この2つが求められることが基本となります。
次回は、この2つの考え方を用いて標準~応用問題を解いていきたいと思います。





